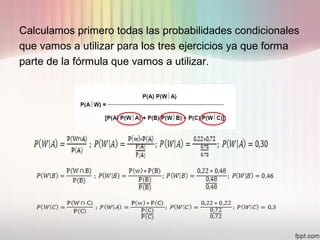
Este documento presenta los pasos para calcular probabilidades condicionadas y aplicar el teorema de Bayes a tres ejercicios. Primero se calculan las probabilidades de déficit alimentario, eliminación e higiene entre pacientes diabéticos. Luego, usando el teorema de Bayes, se calcula la probabilidad de que un individuo al azar tenga cada déficit si padece diabetes. Los resultados son 0.33, 0.33 y 0.34 respectivamente. Finalmente, se representa la situación con un diagrama de Venn.

1. Seminario 7.
Ejercicios de probabilidad simple.
Ejercicios de probabilidad condicionada.
Ejercicios de aplicación del teorema de Bayes.
Mª Dolores Parrilla Rodríguez. 1ºB.
Enfermería. Grupo 7.

2. Tareas a realizar.
Documéntate buscando en la bibliografía sobre los déficit de
autocuidados en alimentación , higiene y eliminación que tiene
los pacientes con DM II.
1. Calcular la probabilidad de P(A│W) que un individuo
elegido al azar.
2. Calcular la probabilidad de averiguar: P(B│W) y P(C│W).
3. Representa la situación en un diagrama y explícalo.
4. Cuélgalo en tu blog portafolio.

3. Utilizaremos este documento como
base de nuestra investigación.

4. Datos que utilizaremos

5. ¿Cómo se haría?
• Llamaremos A a las personas con déficit alimentario, que
engloba el 100% consume alimentos a bases de pastas,
harinas y carbohidratos, 90% tienen antecedesntes
hereditarios de obesidad y 80% no tiene dentadura
completa. Si todo esto lo traducimos a probabilidad quedaría
una cosa así:
P(A)= 1*0,9*0,8 = 0,72.
• Llamaremos W al conjunto de personas diabéticas mellitus
tipo 2.La prevalencia fue a priori 22,2%, que en probabilidad
es:
P(W)= 0,22.

6. • Llamaremos B a las personas que tienen problemas con la
eliminación. Son el 80% manifestaron estreñimiento y el 60%
tomaban laxante. Entonces la probabilidad es :
P(B)= 0,8*0,6= 0,48.
• Llamaremos C a las personas con déficit de higiene, que estaría
formado por 90% que desconocía el corte correcto de las uñas de
los pies, 98% presentaba piel seca. En probabilidad quedaría de la
siguiente forma:
P(C) = 0,9*0,98= 0,72.
Todas estas probabilidades se a calculado gracias a la regla de
multiplicidad.
Una vez que sabemos las probabilidades expuestas arriba,utilizaremos
el teorema de Bayes para calcular la probabilidad de que un individuo
al azar tenga un déficit en la alimentación, déficit de higiene y de
eliminación dado que padezca una DM.

7. Teorema de Bayes
Permite calcular la probabilidad de que un paciente
determinado padezca una determinada enfermedad una
vez dado un o unos síntomas concretos.
Se utiliza la siguiente formula:

8. Calculamos primero todas las probabilidades condicionales
que vamos a utilizar para los tres ejercicios ya que forma
parte de la fórmula que vamos a utilizar.

9. Calcular la probabilidad de P(A│W) que
un individuo elegido al azar.
La probabilidad de que un individuo al azar tenga un
déficit en la alimentación dado que padezca una DM es
del 0,33.

10. Calcular la probabilidad de averiguar:
P(B│W).
La probabilidad de que un individuo al azar tenga un déficit
de eliminación dado que padezca una DM es de 0,33.

11. Calcular la probabilidad de averiguar:
P(C│W).
La probabilidad de que un individuo al azar tenga un
déficit de higiene dado que padezca una DM es de
0,34.

12. Representa la situación en un diagrama
P(A)
0,72
P(B)
0,48
P (C)
0,72
DM
0,22

13. Explicación del diagrama de Venn.
• De color rojo se representa solo el deficit alimentario,
que es 0,72 .
• De color verde se representa solo los problemas de
eliminación, que es 0,48 .
• De color amarillo se representa solo el déficit de higiene,
que es de 0,72.

14. FIN!!!