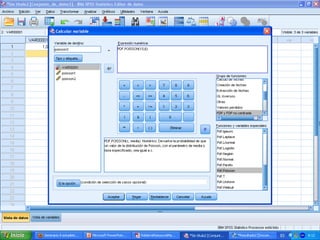
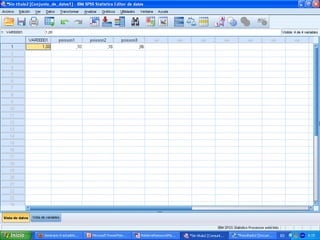
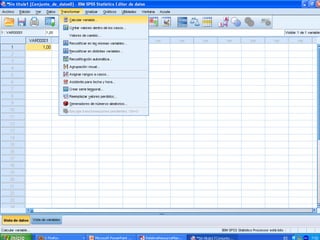
El documento presenta ejercicios sobre distribuciones binomiales y de Poisson. En el ejercicio binomial se calculan probabilidades asociadas al número de pruebas evaluadas correctamente. En el ejercicio de Poisson se calculan probabilidades de muertes por cáncer de pulmón en periodos de tiempo determinados.

1. Irene Mallén Muñoz.

2. *EJERCICIO BINOMIAL

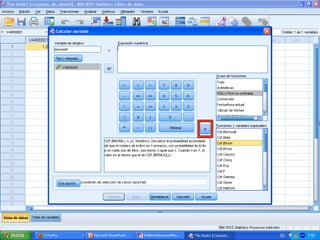
5. a) 60 o menos estén correctamente evaluadas:
P[60 o menos pruebas estén correctamente
evaluadas] = P[X ≤ 60]

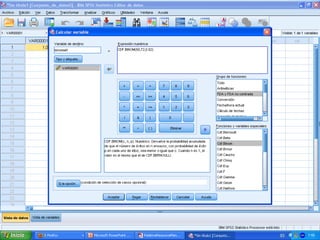
8. b) Menos de 60 estén correctamente
evaluadas:
P[menos de 60 pruebas estén
correctamente evaluadas] = P[X < 60] =
P[X ≤ 59]

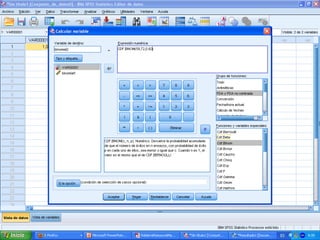
10. c) Exactamente 60 estén correctamente
evaluadas:
P[exactamente 60 estén correctamente
evaluadas] = P[X = 60]

13. *EJERCICIO DE POISSON

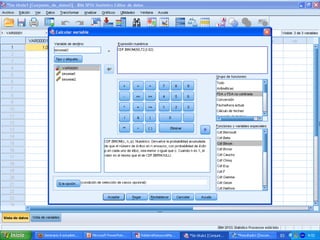
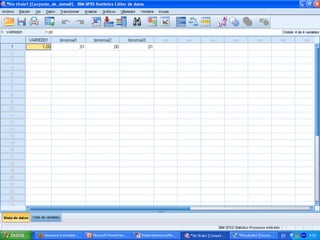
15. a) Haya exactamente 10 muertes por
cáncer de pulmón en un año.
P[ Haya exactamente 10 muertes
por cáncer de pulmón en un año] =
P[X = 10]

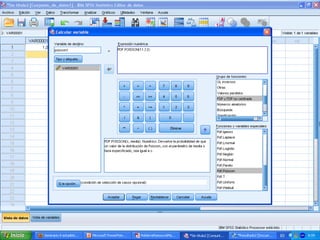
17. b) 15 o más personas mueran a causa de
la enfermedad durante un año.
P[más de 15 personas mueran a causa
de la enfermedad durante un año] =
P[X > 15] = 1 - P[X ≤ 15]

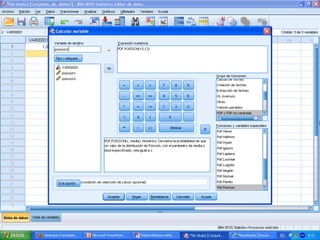
19. c) 10 o menos personas mueran a causa de
la enfermedad en 6 meses. Se define una
nueva variable, Y = ”Nº de muertes por
cáncer de pulmón en seis meses”.Esta
variable aleatoria tiene distribución de
Poisson de parámetro λ = 6. A partir de
aquí se calcula la probabilidad que se pide.
P[10 o menos personas mueran a causa
de la enfermedad en 6 meses] = P[Y ≤
10]