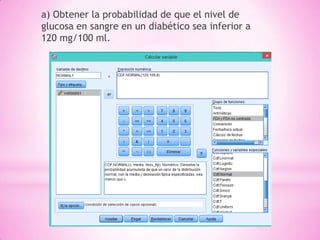
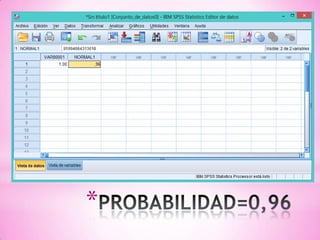
El documento presenta dos problemas relacionados con distribuciones de probabilidad. El primer problema trata sobre una distribución normal para el nivel de glucosa en sangre de diabéticos, calculando la probabilidad de que sea inferior a 120, el porcentaje entre 90-130, y el valor para el 25% inferior. El segundo problema trata sobre una distribución de Poisson para muertes anuales por cáncer de pulmón, calculando la probabilidad de 10 muertes exactas, 15 o más muertes, y 10 o menos muertes en 6 meses.

1. ANDREA MOLERO SÁNCHEZ.
1º ENFERMERÍA MACARENA.
ESTADÍSTICA Y TICs.
*SEMINARIO 8.
DISTRIBUCIONES DE
PROBABILIDAD Y
DENSIDAD.

2. *
*1º- TRANSFORMAR.
*2º- CALCULAR VARIABLE.
*3º- SELECCIONAR GRUPO DE FUNCIONES.
*4º- SELECCIONAR FUNCIONES Y VARIABLES
ESPECIALES.

3. *

4. *

5. *PROBLEMA 1.
MODELO NORMAL.
*Se ha estudiado el nivel de glucosa en sangre
en ayunas en un grupo de diabéticos. Esta
variable se supone que sigue una distribución
Normal:
- media 106 mg/100 ml y
- desviación típica 8 mg/100 ml.

6. *PREGUNTAS
PROBLEMA 1.
*SE PIDE:
a) Obtener la probabilidad de que el nivel de glucosa en
sangre en un diabético sea inferior a 120 mg/100 ml.
b) ¿Qué porcentaje de diabéticos tienen niveles de
glucosa en sangre comprendidos entre 90 y 130 mg/100
ml?
c) Hallar el valor de la variable caracterizado por la
propiedad de que el 25% de todos los diabéticos tiene un
nivel de glucosa en ayunas inferior a dicho valor.

7. a) Obtener la probabilidad de que el nivel de
glucosa en sangre en un diabético sea inferior a
120 mg/100 ml.

8. *

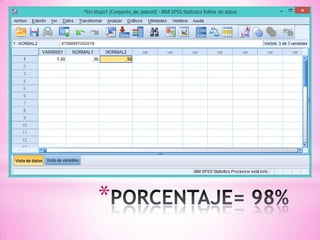
9. b) ¿Qué porcentaje de diabéticos tienen niveles de glucosa en sangre
comprendidos entre 90 y 130 mg/100 ml?
P[Niveles comprendidos entre 90 y 130] = P[90 ≤ X ≤ 130] = P[X ≤ 130] - P[X < 90]

10. *

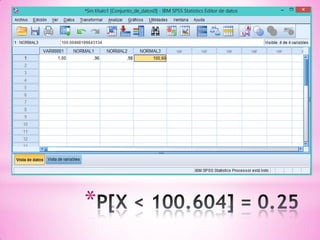
11. c) Hallar el valor de la variable caracterizado por la propiedad de
que el 25% de todos los diabéticos tiene un nivel de glucosa en
ayunas inferior a dicho valor.
Se pide calcular un valor de la distribución, x, tal que P[X < x] = 0.25

12. *

13. *PROBLEMA 2.
*En una cierta población se ha observado
que el número medio anual de muertes por
cáncer de pulmón es 12. Si el número de
muertes causadas por la enfermedad sigue
una distribución de Poisson, calcular las
siguientes probabilidades:

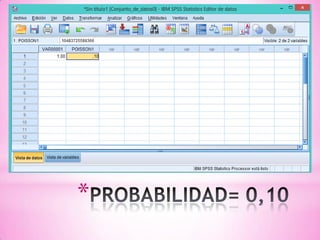
14. *A) HAYA EXACTAMENTE 10 MUERTES POR CÁNCER DE PULMÓN EN UN AÑO.
P[ Haya exactamente 10 muertes por cáncer de
pulmón en un año] = P[X = 10]

15. *

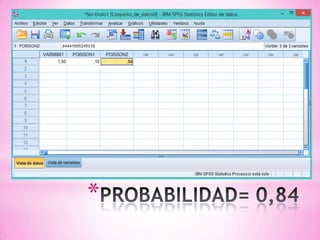
16. *B) 15 O MÁS PERSONAS MUERAN A CAUSA DE LA ENFERMEDAD
DURANTE UN AÑO.
P[más de 15 personas mueran a causa de la enfermedad durante un
año] = P[X > 15] = 1 - P[X ≤ 15]

17. *

18. *C) 10 O MENOS PERSONAS MUERAN A CAUSA DE LA
ENFERMEDAD EN 6 MESES.
Se define una nueva variable, Y = ”Nº de muertes por cáncer
de pulmón en seis meses”.
Esta variable aleatoria tiene distribución de Poisson de
parámetro λ = 6. A partir de aquí se calcula la probabilidad
que se pide.
P[10 o menos personas mueran a causa de la enfermedad
en 6 meses] = P[Y ≤ 10]

19. *FIN.