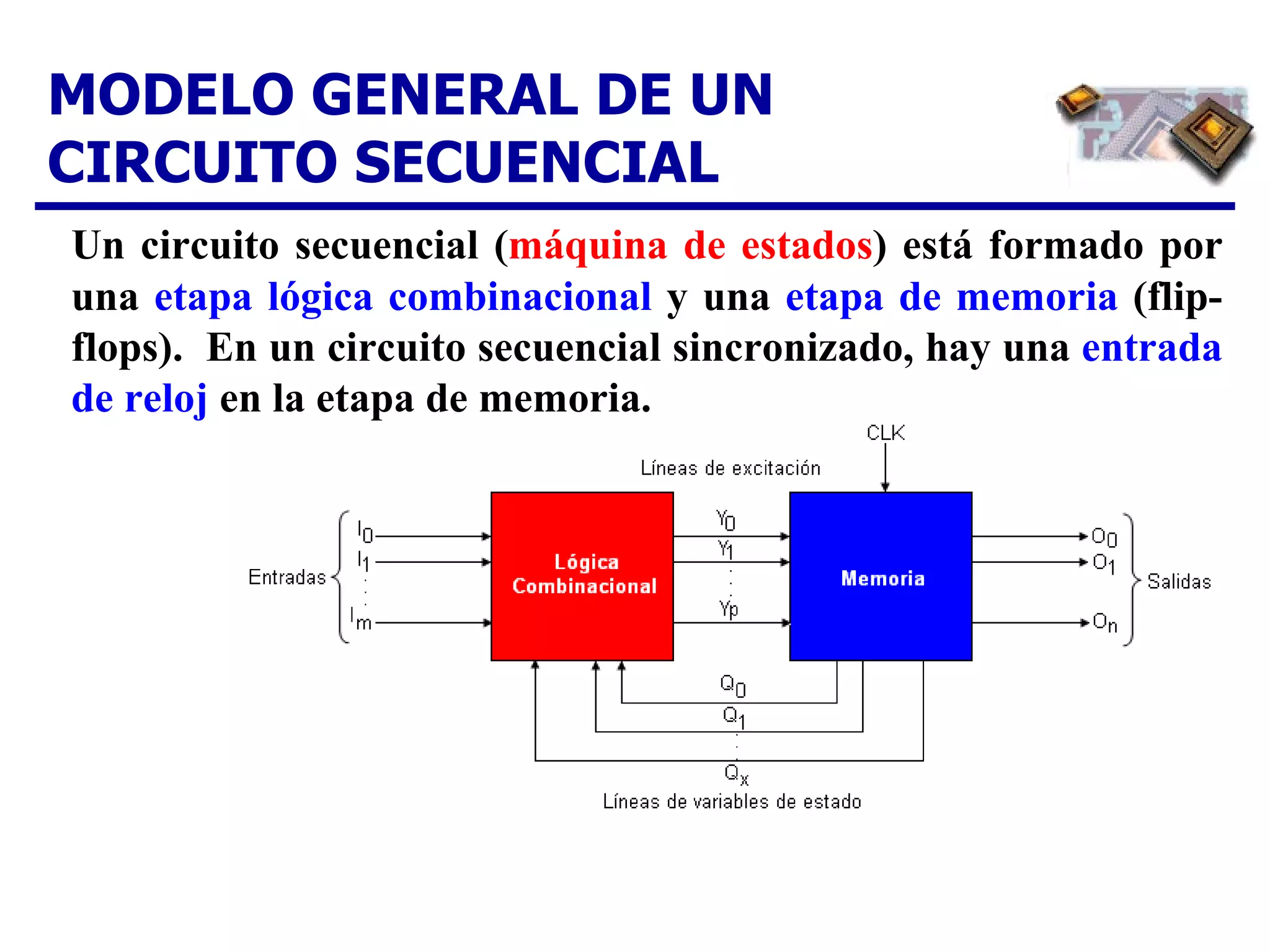
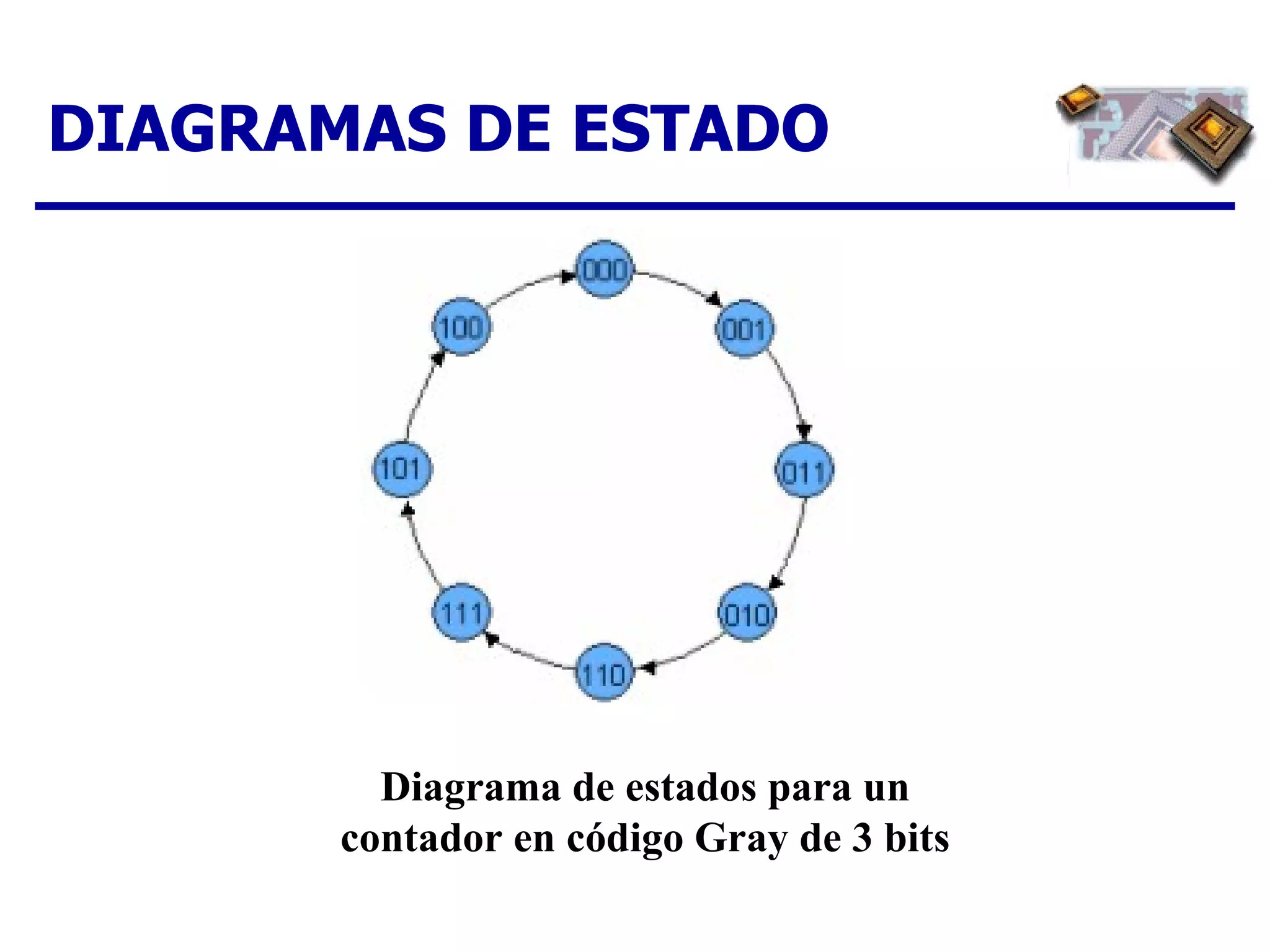
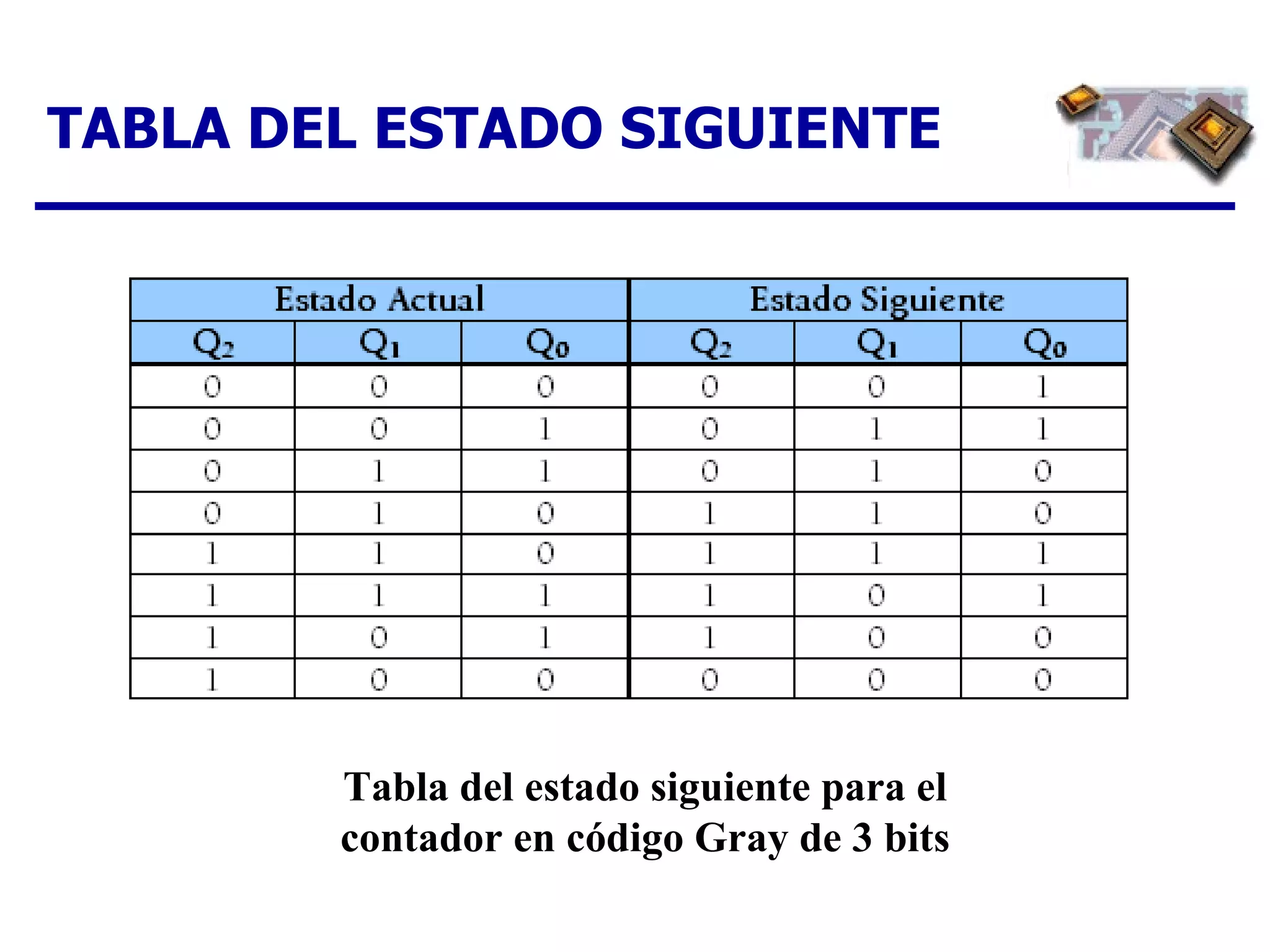
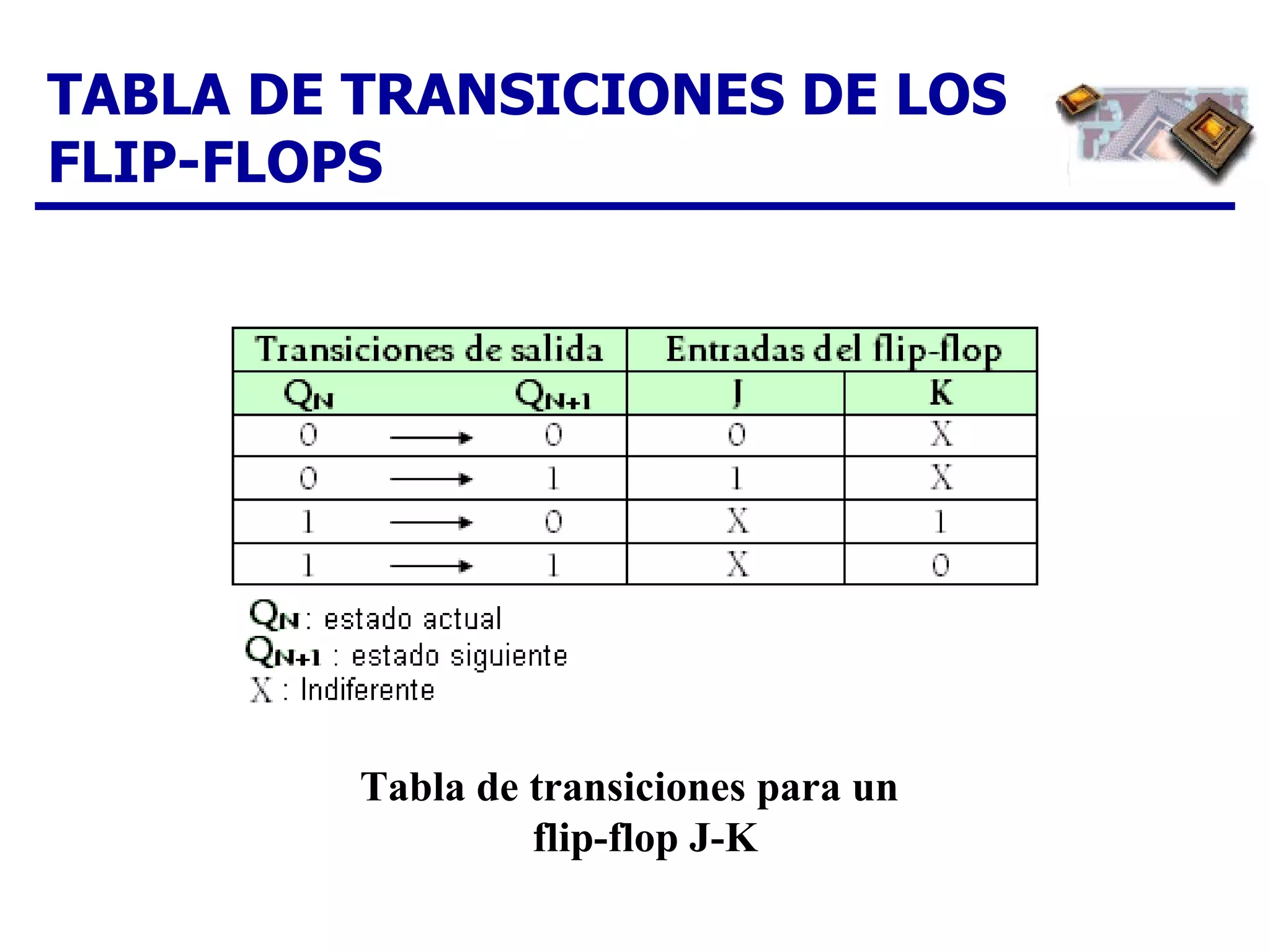
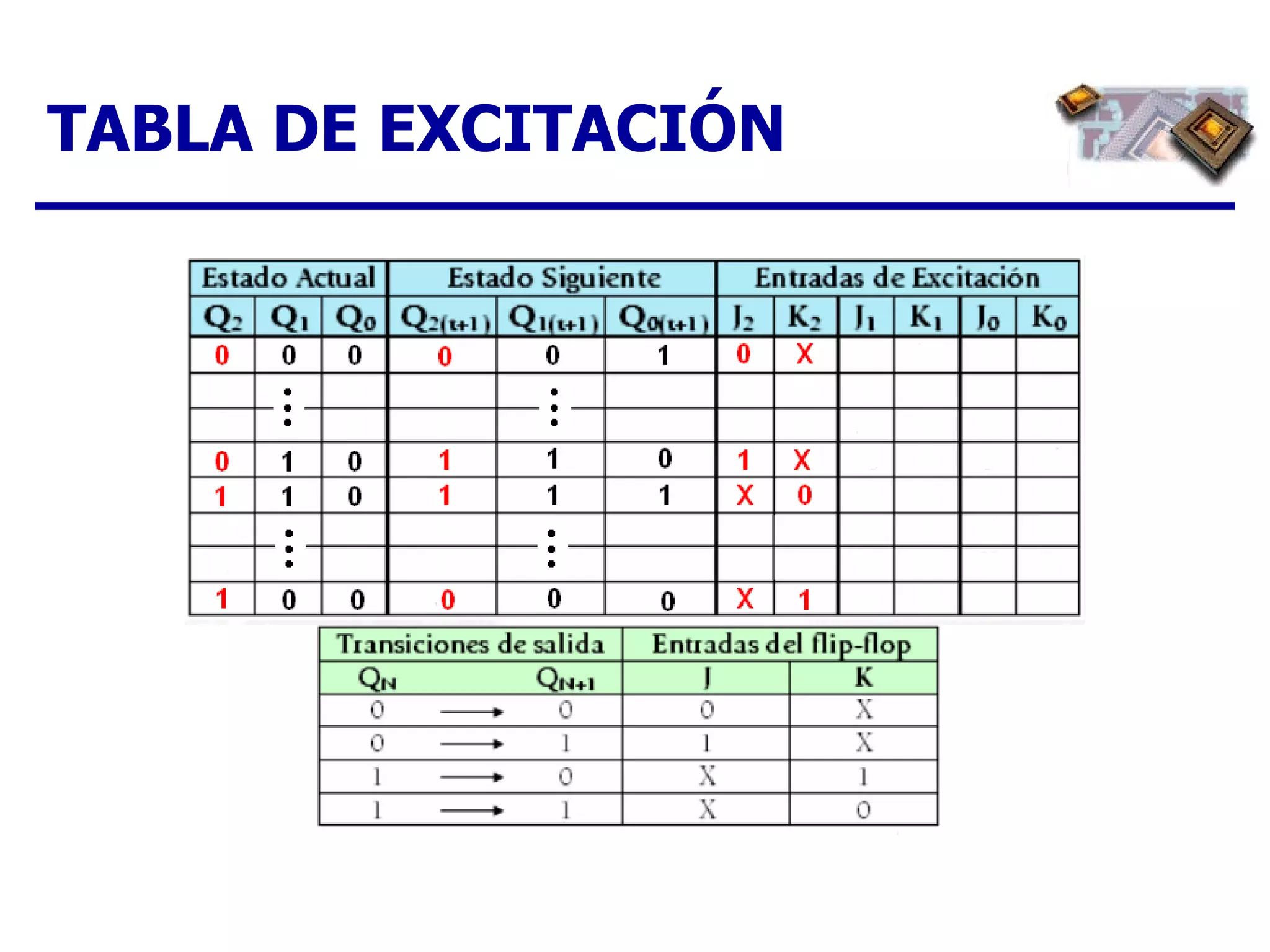
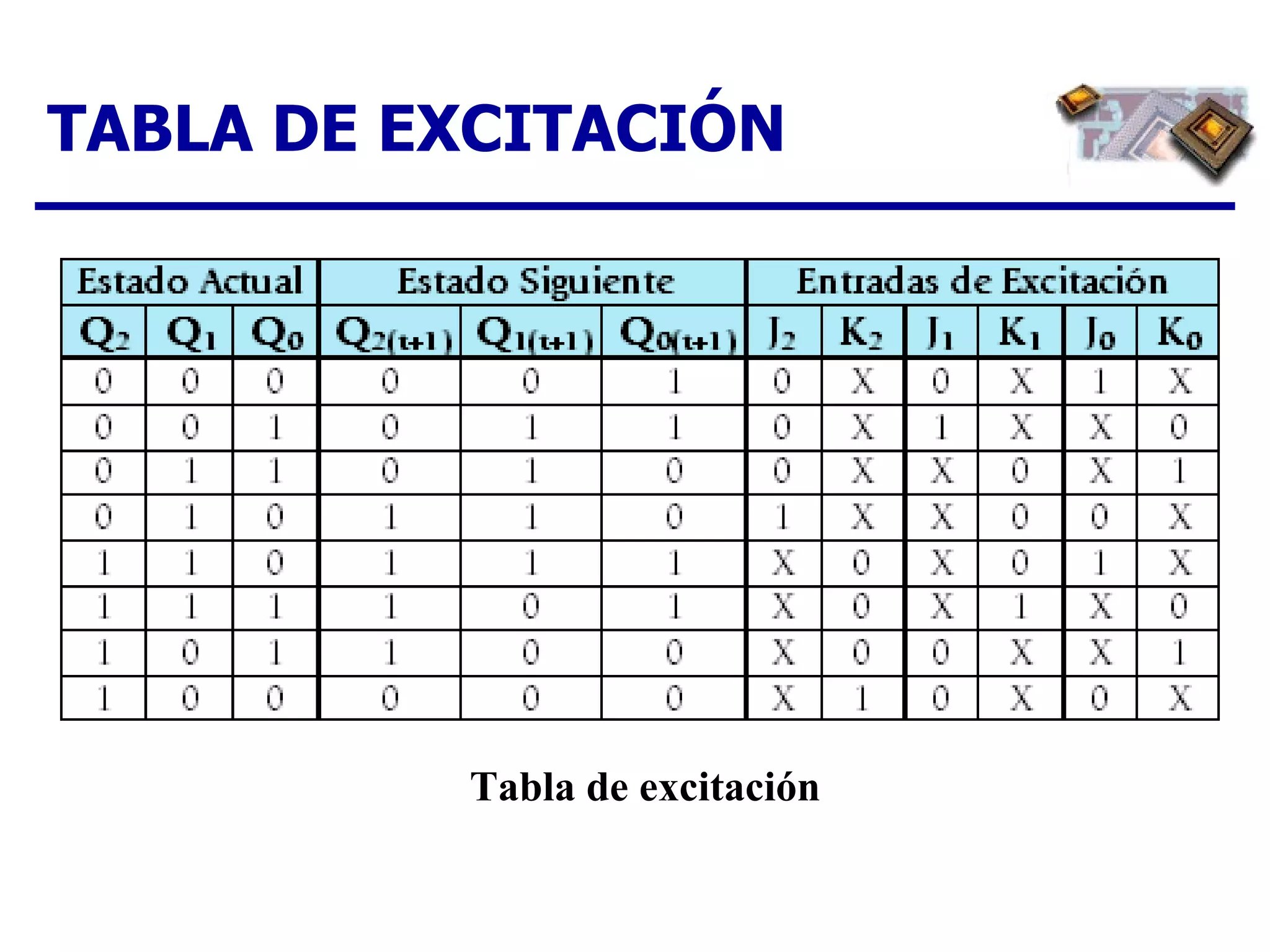
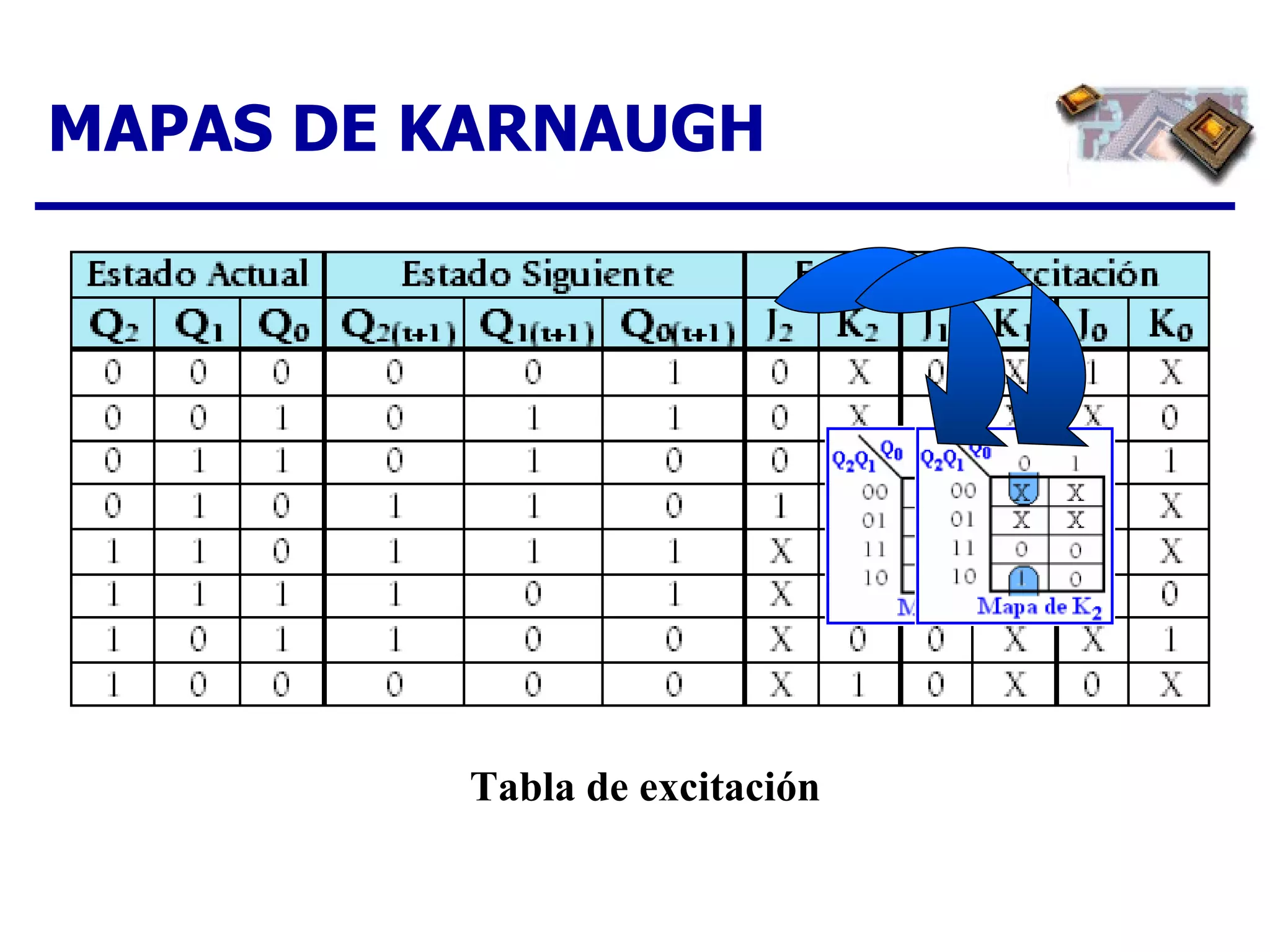
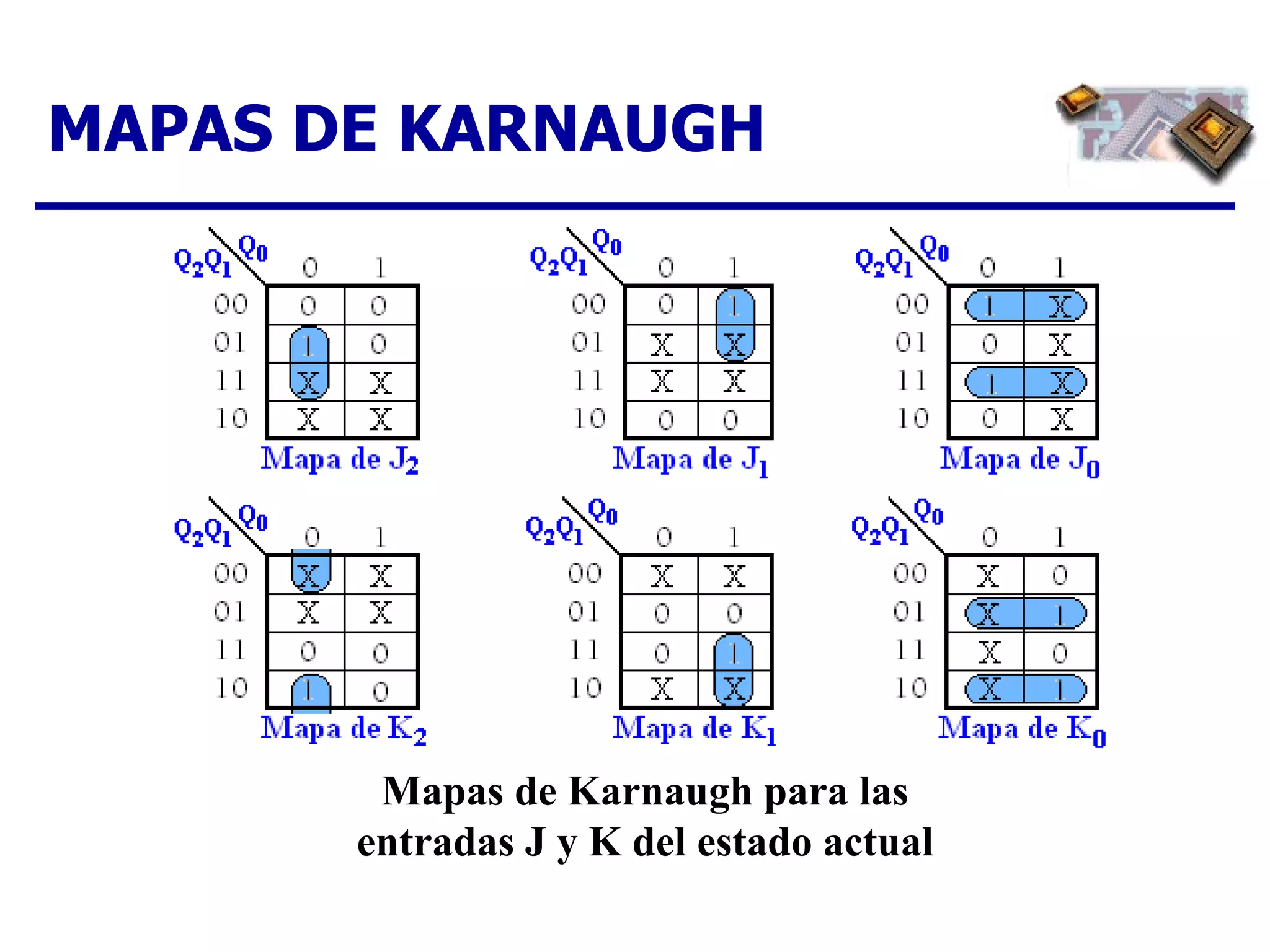
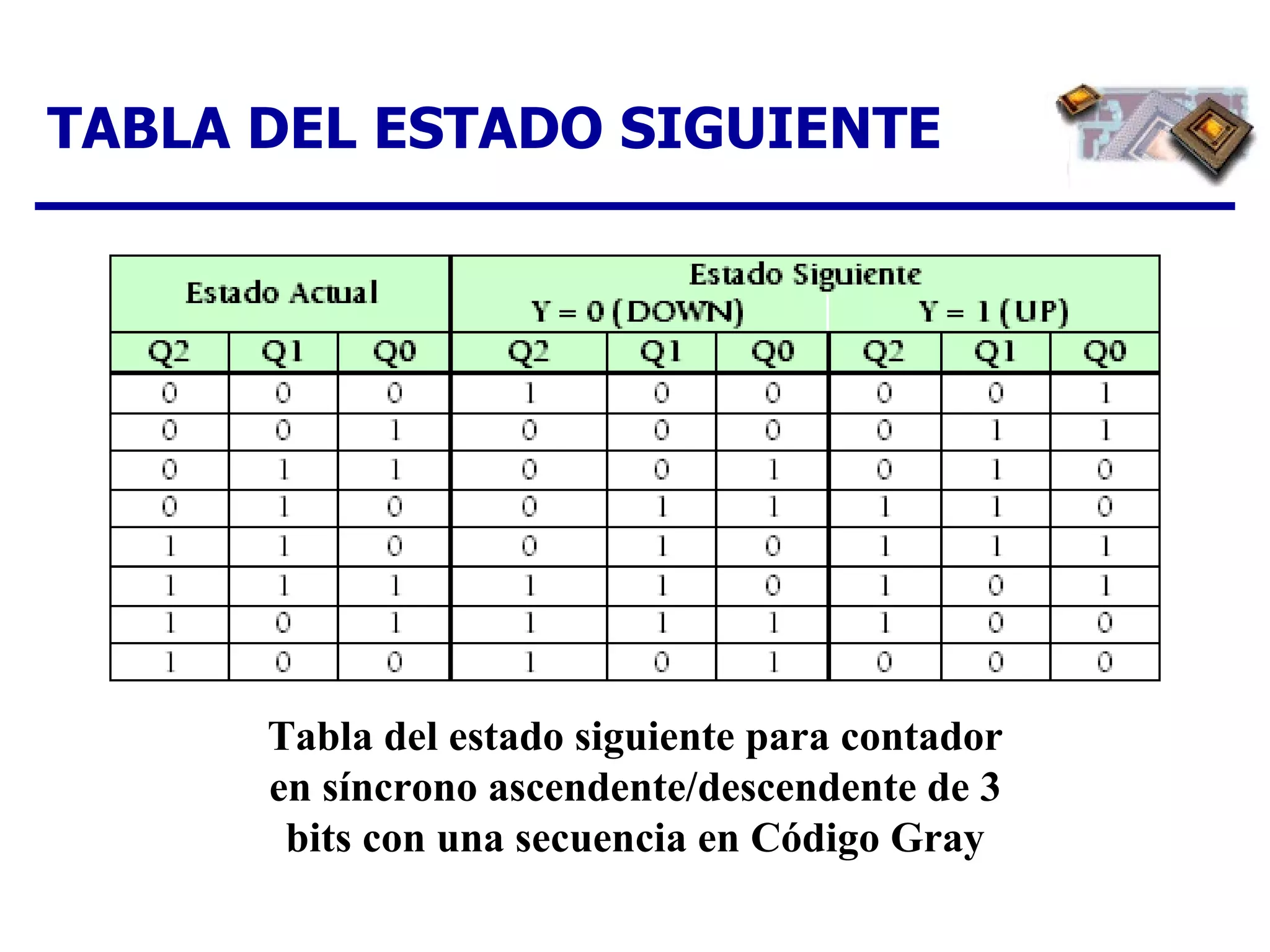
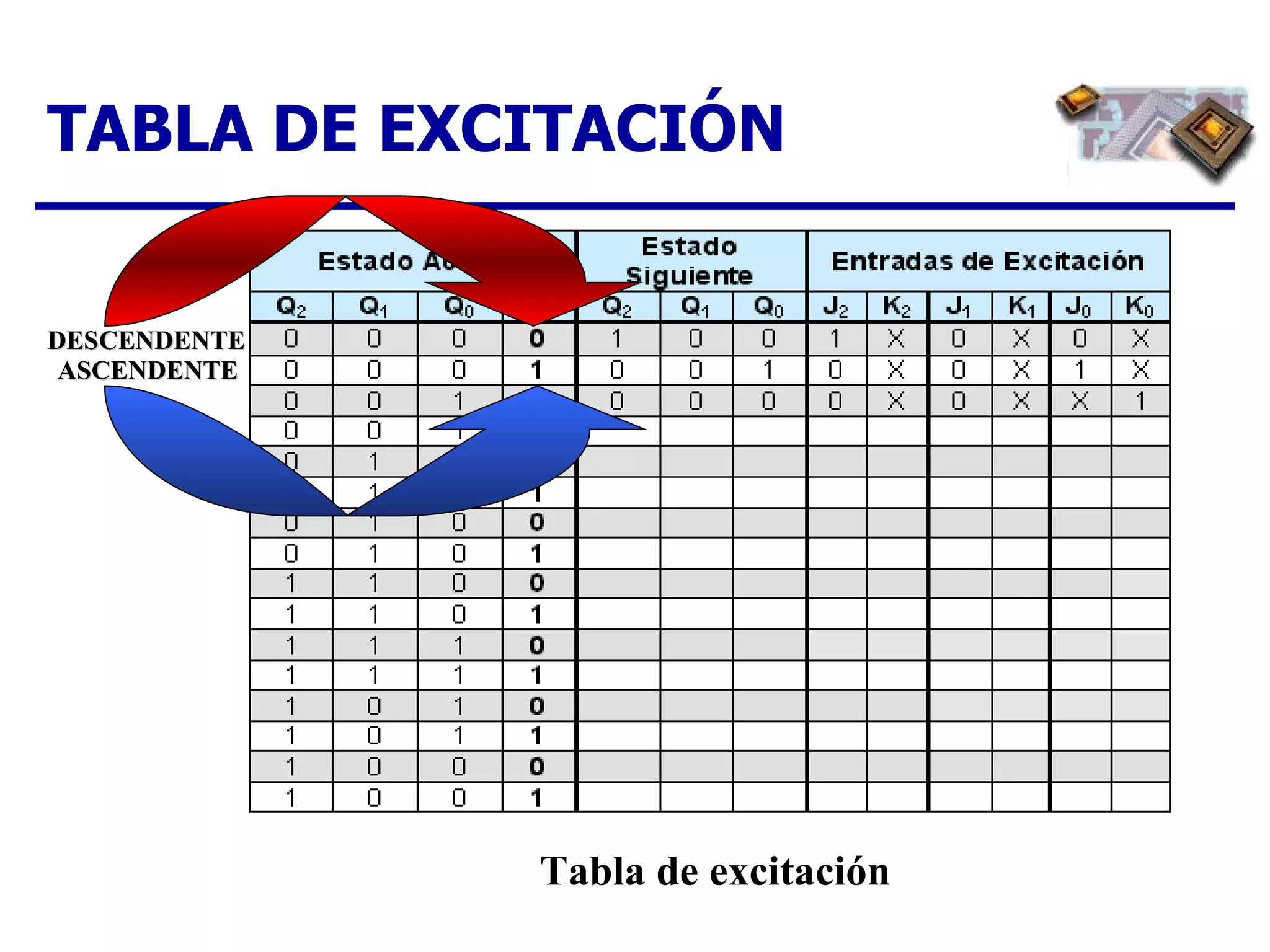
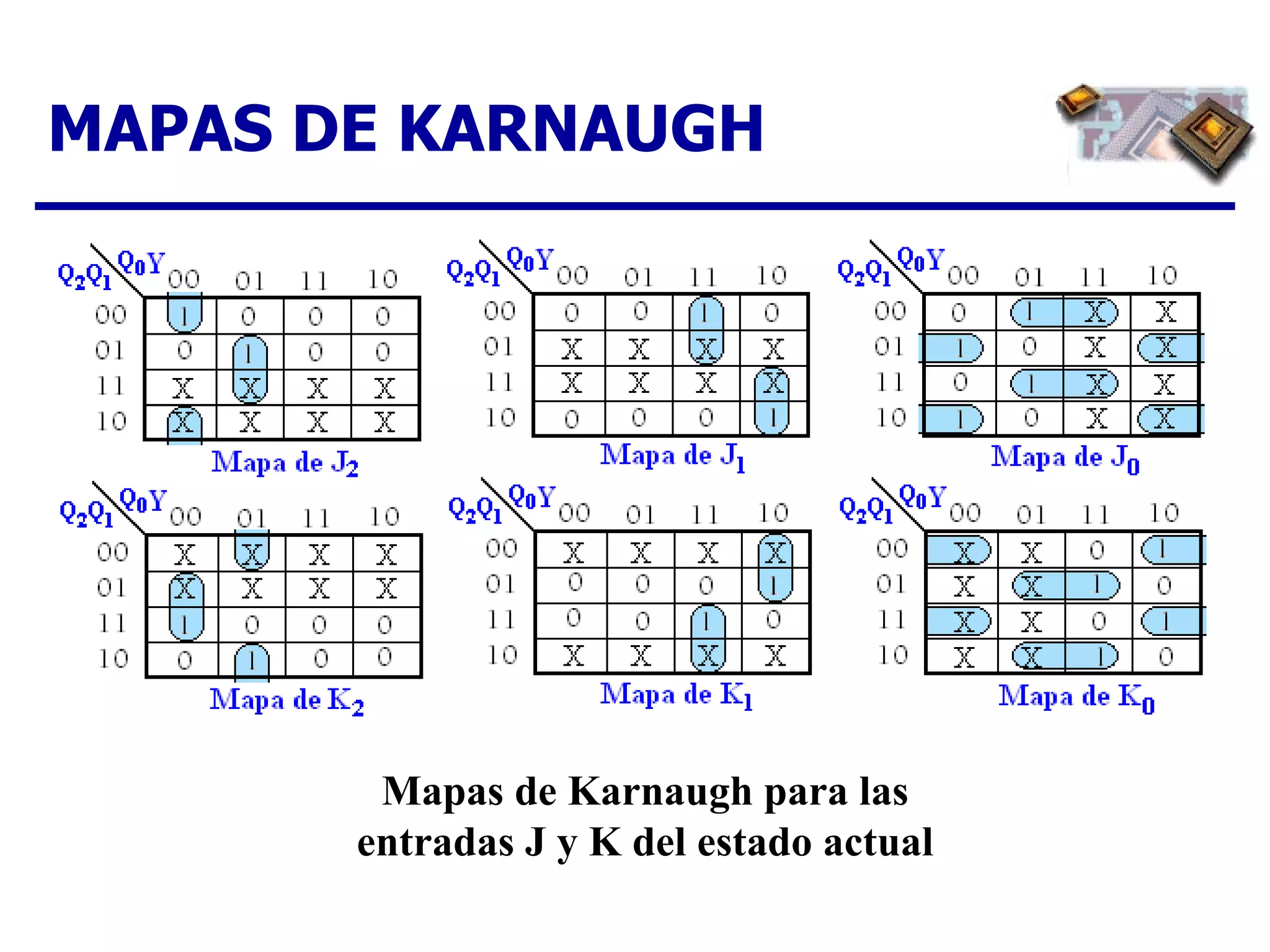
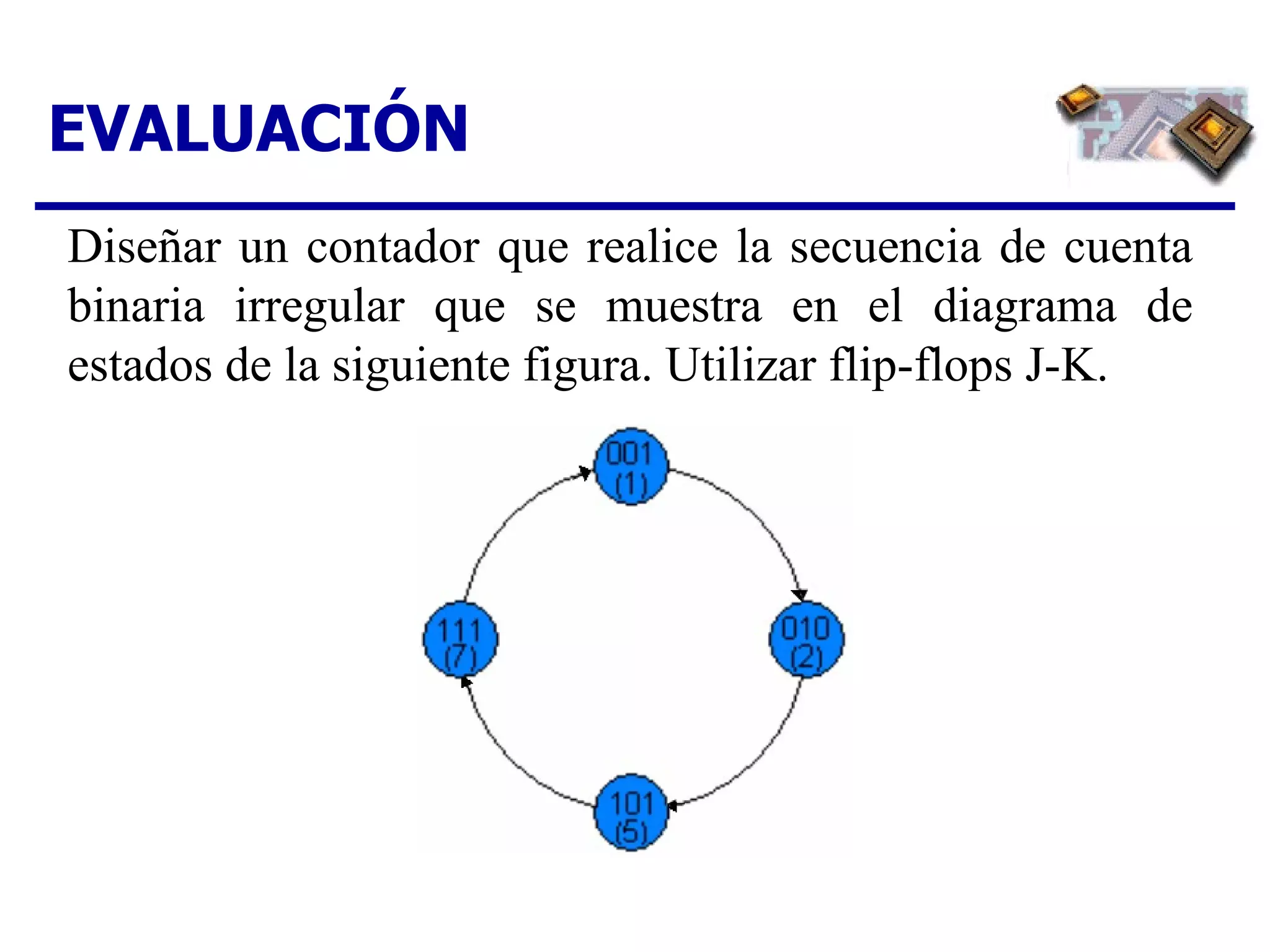
El documento describe los pasos para diseñar un contador síncrono, incluyendo la creación de un diagrama de estados, tabla de estados siguientes, tabla de excitación, mapas de Karnaugh y expresiones lógicas para implementar el contador para una secuencia dada. Se provee un ejemplo completo del diseño de un contador ascendente/descendente de 3 bits con secuencia en código Gray.