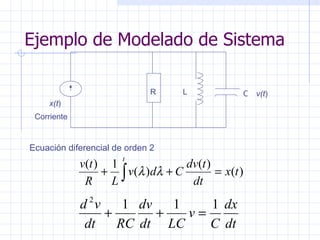
Este documento trata sobre sistemas lineales invariantes en el tiempo. Explica que la respuesta de un sistema LTI a una entrada es la convolución de la entrada con la respuesta al impulso del sistema. También describe cómo modelar sistemas usando bloques básicos como sumadores e integrales para simular ecuaciones diferenciales de cualquier orden.

1. SISTEMAS LINEALES INVARIANTES EN EL TIEMPO Se ñ ales y Sistemas

2. Respuesta al Impulso de un Sistema LTI La respuesta de un sistema lineal invariante en el tiempo con respuesta al impulso h(t) a la entrada x (t) es la convoluci ó n de estas se ñ ales. La respuesta al impulso, h(t), de un sistema lineal invariante en el tiempo, es la respuesta del sistema a un impulso unitario aplicado en la entrada al tiempo cero. El sistema es invariante en el tiempo, entonces, la respuesta al impulso aplicado en alg ú n tiempo diferente de cero, sea este t=  , es simplemente h(t-  ).

3. Ejemplo 1 Encontrar la respuesta al impulso de un sistema modelado por la ecuaci ó n diferencial donde x(t) es la entrada y y(t) es la salida Si x(t) =  (t) resulta la respuesta para y(t) = h(t). Para t>0,  (t)=0, de tal manera que la ecuaci ó n diferencial para la respuesta al impulso es Asumiendo la soluci ó n de la forma h(t) = Aexp(pt) y sustituyendo en la ecuaci ó n para h(t ), se obtiene que La cual se satisface si p = 1/  o

4. Ejemplo 1 Para determinar el valor de A se requiere la condici ó n inicial para h(t). El sistema no esta excitado para t<0. Por lo tanto, de la definici ó n de la respuesta al impulso, h(t)=0, t<0. Integrando la ecuaci ó n de diferencias en el intervalo de (0 - ,0 + )

5. Ejemplo 2 Considere el sistema con la respuesta al impulso Suponga x(t) = u(t) – Funcion de Paso Unitario, aplicando y(t)=x(t)*h(t)=h(t)*x(t) Se puede obtener la salida:

6. Integrales de Superposici ó n En el ejemplo 2, la respuesta al escal ó n unitario del circuito RC es simplemente la integral de la respuesta al impulso del circuito. ¿ Puede entonces, la respuesta de cualquier sistema a una entrada arbitraria ser expresada en t é rminos de su respuesta a la funci ó n escal ó n unitario? Considere la integral de superposici ó n en t é rminos de la respuesta al impulso. Empleando la f ó rmula de integraci ó n por partes se tiene:

7. Integrales de Superposici ó n Con u=x(t-  ) y dv=h(  )d  La respuesta de un sistema para cualquier entrada x(t) es la convoluci ó n de su derivada con la respuesta al escal ó n unitario. Esto es conocido como Integrales de Duhamel ’ s.

8. Funci ó n de Respuesta en el dominio de la Frecuencia Si la entrada a un sistema LTI es una senoidal de frecuencia  rad/s, la respuesta de estado estable es una senoidal con la misma frecuencia pero con amplitud multiplicada por un factor A(  ) y un desplazamiento en fase de  (  ) radianes. La funci ó n compleja de frecuencia es Llamada funci ó n de respuesta en el dominio de la frecuencia; A(  ) y  (  ) son referidas como funciones amplitud y fase la de respuesta. La funci ó n de respuesta en el dominio de la Frecuencia caracteriza completamente la respuesta de estado estable de un sistema LTI para una senoidal o funci ó n fasor e j  t . La salida de estado estable de un sistema LTI es de la misma forma que su entrada cuando su entrada es e j  t .

9. Estabilidad de Sistemas Lineales Una de las consideraciones en cualquier dise ñ o de sistema es el criterio de estabilidad. Un sistema es estable BIBO si y solo si para cualquier entrada limitada resulta en una salida limitada. Entrada Limitada -> Salida Limitada (BIBO) Para un sistema lineal invariante en el tiempo se puede obtener una condici ó n de la respuesta al impulso que garantiza la estabilidad BIBO. Para derivar esta condici ó n, consideraremos la f ó rmula de la convoluci ó n que relaciona la entrada y la salida de un sistema LTI.

10. Condici ó n de la Respuesta al Impulso Se sigue que Se sabe que la entrada x(t) es limitada Remplazando x(  ) por M, y cambiando el par á metro de h se tiene la desigualdad As í la salida ser í a limitada si se cumple que:

11. Ejemplo de Sistemas Estables BIBO La respuesta el impulso de este sistema es: Para comprobar la estabilidad utilizamos el criterio de: R i(t) + - + - C y(t) x(t)

12. Ejemplo de Sistema Inestable La respuesta al impulso para este sistema sigue la forma: Substituyendo la respuesta al impulso para este sistema en la integral para comprobar la estabilidad se tiene La integral no converge, la condici ó n de Estabilidad BIBO no se cumple para este sistema. L i(t) + - + - C y(t) x(t)

13. Modelado y Simulaci ó n de Sistemas Los sistemas pueden ser modelados y simulados en t é rmino de varios bloques b á sicos de construcci ó n, que son: sumadores, restadores, multiplicadores constantes integradores. Ecuaciones diferenciales de coeficientes constantes y de orden n puede ser simulada mediante estos componentes. La realizaci ó n de tal simulaci ó n puede tomar dos formas: Anal ó gica : por medio de circuitos amplificadores operacionales que aproximan sumadores e integradores ideales. Programa de Computadora donde la integraci ó n es hecha num é ricamente.

14. Bloques B á sicos de Construcci ó n

15. Modelado y Simulaci ó n de Sistemas Para ver como se puede simular un sistema, ya sea por medio de los amplificadores operacionales o por algoritmos consideremos la ecuaci ó n diferencial de primer orden. Esto es realizado por el siguiente diagrama de bloques. b o   b 1 a x(t) y(t) + + - + dq/dt q(t)

16. Modelado y Simulaci ó n de Sistemas Para mostrar que este caso, tomemos la salida del integrador q(t). Su entrada es dq/dt. En el diagrama dq/dt es Considerando la salida del sumador del lado derecho se tiene que: y=q+b 1 x Diferenciando ambas partes y sustituyendo dq/dt, obtenemos:

17. Ecuaci ó n Diferencial General para un Sistema de orden n De manera similar al caso del primer orden, se puede realizar un sistema de orden n con un diagrama de bloques de la siguiente figura. Y la ecuaci ó n de diferencias ser í a

18. Diagrama de Bloques General para Sistemas de orden n

19. Ejemplo de Modelado de Sistema R C L x(t ) v(t ) Ecuación diferencial de orden 2 Corriente

20. Diagrama de Bloques 1/C ∫  ∫ 1/RC 1/LC + - - x(t) v(t)

21. Implementaci ó n con Amplificadores