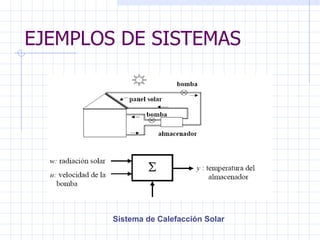
El documento define un sistema como una combinación e interconexión de componentes para realizar una tarea. Matemáticamente, un sistema relaciona una entrada con una salida a través de ecuaciones. Un sistema físico está sujeto a leyes físicas y procesa señales de entrada para generar señales de salida. Los sistemas pueden ser lineales o no lineales, invariantes o variantes en el tiempo, causales o no causales, estables o inestables, con o sin memoria.

1. SISTEMAS

2. DEFINICION DE SISTEMA Un sistema esta definido como una combinaci ó n e interconexi ó n de varios componentes para realizar una tarea deseada.

3. Sistemas Matem á ticamente, un sistema es la relaci ó n funcional entre una entrada "x" y la salida "y". y(t) = T [x(t)] x continua y(n) = T [x(n)] x discreta La representaci ó n normal de un sistema (tiempo continuo) se realiza normalmente a trav é s de ecuaciones diferenciales. Se relacionan la salida y(t) y la entrada x(t) mediante constantes, par á metros y variables independientes (tiempo):

4. Sistemas Un sistema f í sico es un conjunto de dispositivos conectados entre s í , cuyo funcionamiento est á sujeto a leyes f í sicas. Desde otro punto de vista, un sistema es un procesador de se ñ ales. La se ñ al o se ñ ales a ser procesadas forman la excitaci ó n o entrada del sistema. La se ñ al procesada es la respuesta o salida del sistema. El an á lisis de sistemas implica el estudio de la respuesta del sistema a entradas conocidas. La s í ntesis de sistemas se realiza especificando las salidas que deseamos para una entradas dadas y estudiando que sistema es el m á s adecuado ( Identificaci ó n de sistemas). Las se ñ ales observables que son de nuestro inter é s son usualmente denominadas salidas del sistema y las denotaremos con y.

5. Sistemas El sistema est á tambi é n afectado por est í mulos externos. Las se ñ ales externas que pueden ser manipuladas son usualmente llamadas entradas , que denotamos con x , mientras que las que no pueden ser manipuladas son llamadas perturbaciones . Las perturbaciones suelen dividirse en aquellas que pueden medirse directamente y aquellas que se ponen en evidencia s ó lo a trav é s de su influencia en las salidas.

6. Sistemas Sistemas con una sola entrada y una sola salida se denominan SISO (Single-Input/Single-Output), o escalares, o monovariables. Sistemas con varias entradas y varias salidas se denominan MIMO (Multiple-Input/Multiple-Output), o multivariables. Los sistemas no necesariamente est á n restringidos a sistemas f í sicos. Pueden ser biol ó gicos, econ ó micos, computacionales, inform á ticos, sociales, etc.

7. Clasificaci ó n de los Sistemas Lineales y no lineales : Un sistema es lineal si se puede aplicar el principio de superposici ó n, es decir, si y 1 (t)= T [ x 1 (t) ] y y 2 (t) = T [ x 2 (t) ] entonces si el sistema es lineal, se cumplir á que: T [a x 1 (t) + b x 2 (t) ] = a y 1 (t) + b y 2 (t) . Ejemplos: T [ x(t) ] = a x(t) es un sistema lineal. T [ x(t) ] = a x 2 (t) es no lineal T [ x(t) ] = a x(t) + b es un sistema no lineal. A este tipo de sistema se le llama lineal incremental .

8. Clasificaci ó n de los Sistemas Invariante o variante en el tiempo : Un sistema donde y(t) = T [ x(t) ] se dice que es invariante en el tiempo si al excitarlo con x( t - t 0 ) genera y( t - t 0 ). La definici ó n es similar para sistemas discretos. En otras palabras el comportamiento del sistema no cambia con el tiempo. Ejemplo: y(t) =t x(t) es variante en el tiempo . Causal o no causal: Un sistema es causal si la salida no comienza antes de aplicar la excitaci ó n de entrada, es decir si no es anticipativo. La salida para t= t 0 ( ó para n= n 0 ) , solo depende de los valores de entrada para t menor que t 0 (o para n menor n 0 ) y de los valores de la salida para t menor que t 0 ( ó para n menor que n 0 ) Cuando las se ñ ales provenientes de un proceso f í sico son almacenadas, uno puede realizar sobre ella procesamiento de tipo no causal.

9. Clasificaci ó n de los Sistemas Estable o inestable : Un sistema es estable si para entradas limitadas en amplitud, la salida tambi é n es limitada. Ejemplo: Para un sistema integrador, si por ejemplo x(t) = u(t), la salida y(t) crecer á , en principio, hasta el infinito; por lo tanto este sistema es inestable. Sistemas con y sin memoria (Din á micos o Instant á neos) : Un sistema se dice que no tiene memoria si la salida para cada valor de t ( ó n) solo depende de la entrada en ese instante Ejemplos: y(t) = A x(t) es un sistema sin memoria y(t) = x 2 (t) -2x(t) es un sistema sin memoria. y(n) = x(n-2)-x(n)+2x(n-1) define un sistema discreto con memoria.

10. Clasificaci ó n de los Sistemas Sistemas invertibles o no invertibles : Si para entradas diferentes, las salidas tambi é n son diferentes entre s í , el sistema en cuesti ó n se dice que es invertible. Ejemplos: y(t) = A = constante (es no invertible) y(t) = x 2 (t) (es no invertible)

11. EJEMPLOS DE SISTEMAS Sistema de Calefacción Solar

12. EJEMPLOS DE SISTEMAS Sistema mecánico rotacional

13. EJEMPLOS DE SISTEMAS Circuito eléctrico

14. EJEMPLOS DE SISTEMAS Sistema Electromecánico (Motor de Corriente Continua)

15. Representaci ó n de Sistemas La ecuación diferencial relacionando x(t) y y(t) se establece con la Ley de voltaje de Kirchhoff en el lazo indicado por la corriente i(t) . donde y(t) , el voltaje a través del capacitor esta relacionado con la corriente por: Remplazando i(t) en la ecuación anterior, se tiene R i(t) + - + - C y(t) x(t)

16. Representaci ó n de Sistemas Para escribir la relación entrada-salida como una ecuación explicita para y(t) en términos de x(t), primero obtenemos la solución de la ecuación diferencial homogénea: Asumiendo la solución de la forma: donde p=-1/RC.

17. Representaci ó n de Sistemas Para encontrar la solución total utilizamos la técnica de variación de parámetros, el cual consiste en asumir una solución de la forma y h (t) pero con el coeficiente A remplazado por una función del tiempo. Sustituyendo en la ecuación de Kirchhoff