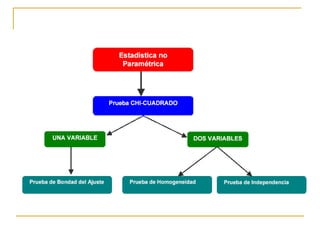
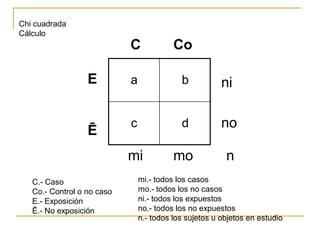
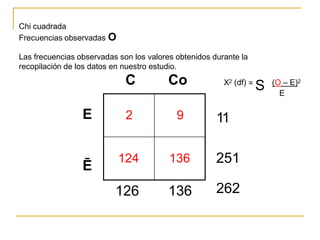
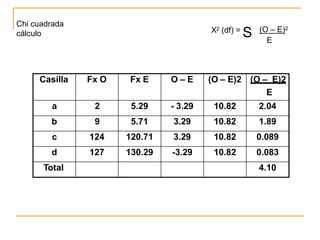
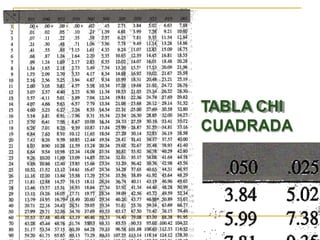
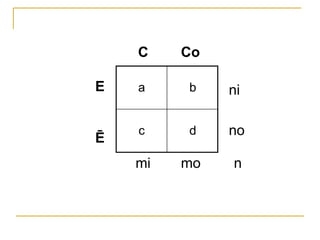
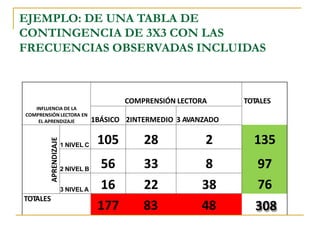
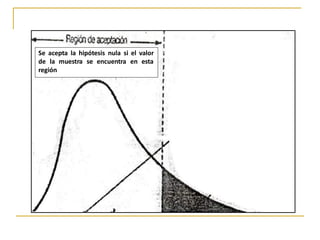
Este documento explica cómo realizar la prueba de chi cuadrado para comparar proporciones independientes. La prueba de chi cuadrado permite determinar si la diferencia observada entre una variable independiente y una variable dependiente es estadísticamente significativa. El documento detalla los pasos para calcular la chi cuadrada, incluyendo cómo obtener las frecuencias esperadas y los grados de libertad, y cómo comparar el resultado con un valor crítico para establecer si se rechaza o no la hipótesis nula. También incluye un ejemplo de

1. LeninH.Cari Mogrovejo
zarlenin@gmail.com

3. X2
Ji2
Chi
cuadrada.
Seutilizaparacompararproporcionesindependientes
endiseñosdeestudioconvariablescualitativas.
Lafrecuenciaesperadadequeocurrauneventosecompara
conlafrecuenciaobservada.
Cuandocorrelacionamoslaformaenquelamodificaciónde
unavariableindependienteinfluyeenlavariabledependientelapruebachicuadradanosinformasiladiferenciaobservadaesestadísticamentesignificativa.Oseaquelamodificación
delavariableindependientesiinfluyeenelresultadoobservado
enlavariabledependiente.

4. Prueba
Chi
cuadrada

5. Chicuadrada.
Fórmula.
X2(df) =S
(O–E)2
E
x2
.-Chicuadrada
df.-
S.-
O.-
grados de libertad
sumade..
eventosobservados
E.-eventosesperados

6. a
b
c
d
Chicuadrada
Cálculo
C
Co
E
ni
no
Ē
mi
mo
n
mi.-todosloscasos
mo.-todoslosnocasos
ni.-todoslosexpuestos
no.-todoslosnoexpuestos
n.-todoslossujetosuobjetosenestudio
C.-Caso
Co.-Controlo
E.-Exposición
nocaso
Ē.-Noexposición

7. 2
9
124
136
Chicuadrada
Frecuenciasobservadas O
Lasfrecuenciasobservadassonlosvaloresobtenidosdurantela
recopilacióndelosdatosennuestroestudio.
C
Co
X2(df)
(O –E)2
=S
E
E
11
251
Ē
262
126
136

8. Chicuadrada
¿Cómoobtenerlasfrecuenciasesperadas E.?
X2(df)
(O–E)2
=S
E(a)=(mi)(ni)/n=126x11/262=5.29
E
E(b)=(mo)(ni)/n=136x11/262=5.71
E(c)=(mi)(no)/n=126x251/262=120.71
E(d)=(mo)(no)/n=136x251/262=130.29
¿Cómoobtenerlosgradosdelibertaddf.?
Enestecasohaydosrenglones
ydoscolumnas.
(2–1)(2-1) =1x1=1
df=(F–1) (C –1)
F=FILAS
C=COLUMNAS

9. Casilla
FxO
FxE
O–E
(O–E)2
(O–E)2
E
a
2
5.29
-3.29
10.82
2.04
b
9
5.71
3.29
10.82
1.89
c
124
120.71
3.29
10.82
0.089
d
127
130.29
-3.29
10.82
0.083
Total
4.10
Chicuadrada
cálculo
X2(df) =S
(O–E)2
E

10. Chicuadrada
Cálculo
ElresultadosecontrastaráconelestadísticoChi obtenidode lastablascon1gradodelibertadyuna significanciade0.05(aenlastablas)
X2(df)=S
(O –E)2
E
Aestedatoseledenominavalorcríticoyesiguala3.841
Secomparaconelresultadoobtenidodeldesarrollo
lafórmula( 4.10)
de
Sielvalorobtenidoaldesarrollarlafórmula(4.10)es
mayor
alvalorcrítico(3.841)seconcluyequeladiferenciade
casosobservadosenlosgruposesdiferenteyquese
debealefectodelaexposiciónenestudio.
Sielvalorobtenidohubierasidomenoralvalorcrítico
seconcluiríaqueelnúmerodecasosenlosgrupos
expuestoynoexpuestosonestadísticamenteiguales.

11. TABLACHI
CUADRADA

12. a
b
c
d
C
Co
E
ni
no
Ē
mi
mo
n

13. X2
Pruebadesignificanciade
Cuandoseanalizanlosresultadosdeuncruce,
senecesitaconocersilosresultadosobtenidossedesvíansignificativamentedelosresultadosesperados.
LapruebadeChi-cuadrado seusapara compararlosresultadosobservadosdelos


resultadosesperados
poruna hipótesisysila
desviaciónobtenidanoessignificativaypuede
atribuirse
alazar o essignificativayotras
variablesdiferentesal azarestáninfluyendoen
nuestrosresultados.

14. INFLUENCIADE LA COMPRENSIÓNLECTORAEN ELAPRENDIZAJE
COMPRENSIÓNLECTORA
TOTALES
1BÁSICO
2INTERMEDIO
3AVANZADO
APRENDIZAJE
1NIVELC
105
28
2
135
97
76
2NIVELB
56
33
8
3NIVELA
16
22
38
TOTALES
1778348
308
EJEMPLO:DE UNATABLA DE
CONTINGENCIADE 3X3 CONLAS
FRECUENCIASOBSERVADASINCLUIDAS

15. COMPROBACIÓN DE HIPÓTESIS
CONLA CHI CUADRADA
PASO 1:FORMULACIÓNDE HIPÓTESIS

Ho:
Lacomprensiónlectora
NO influye

positivamenteenelaprendizaje
H1:
Lacomprensiónlectora
influye

positivamenteenelaprendizaje
HIPÓTESISDELINVESTIGADOR

16. PASO 2:NIVELDESIGNIFICANCIA

Niveldesignificancia
α=0.05


alfa=
0.05


17. PASO 3ESTABLECER
LIBERTAD
LOS
GRADOS
DE

GL=(F-1)(C-1)
GL=(3-1)(3-1) GL=(2)(2)=4

18. PASO 4:ELECCIÓNDELAPRUEBA
ESTADÍSTICA

HALLAR


19. Seaceptalahipótesisnulasielvalor
de la muestra se encuentra en esta
región

20. Valor
gl
Chi-cuadradodePearson
SEHALLAELVALORDELA
CHICUADRADA

21. PASO5
intervalo
ANÁLISISDEDATOS
El
valor
de
la
Chi-cuadradoqueda
FUERA
del

deaceptación
dela
hipótesis
nula
(Ho),
lo
cual
determina
que
seRECHAZA
la
hipótesis
alternativa
nula
(H1),
yse
que
ACEPTA
la
hipótesis
corresponde
a
ladel
investigador
ElvalordelaChi-cuadradoquedaDENTROdel

intervalo
de
aceptación
de
la
hipótesis
nula
(Ho),
lo
cualdetermina
que
se
ACEPTA
la
hipótesis
alternativa
nula
(H1),
y
seRECHAZA
la
hipótesis
que
corresponde
a
la
delinvestigador

22. Muchasgracias
LeninH.CariMogrovejo
Cel.959966199zarlenin@gmail.comlenin_9966199@hotmail.com