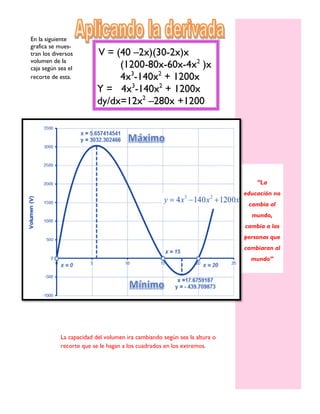
El documento describe tres problemas relacionados con la fabricación de una caja de cartón rectangular sin tapa. El primer problema pregunta cuánto deben medir los cuadrados recortados en cada esquina para que el volumen de la caja sea máximo. Al resolver este problema, se determina que la medida óptima es 5.6574 cm. El segundo problema explica cómo calcular el volumen de la caja en función del tamaño del recorte. El tercer problema define la derivada matemática y su uso para encontrar puntos máximos y mínimos de una función relacionada con el vol

1. PROCESOS INDUSTRAILES
UNIVERSIDAD
TECNOLÓGICA DE
TORREÓN
Problema de la caja 2
Martes 12 de Noviembre del 2013
Puntos de interés
especial:
 Se le llama CRECIEN-
TE cuando la curva va
aumentado.
 El punto mas alto, se
le conoce como ESTACIONARIA.
 Se le llama DECRE-
CIENTE
CONTENIDO:
El problema de la caja de cartón
Se dispone de una
pieza rectangular
de cartón.
° Con este material
se va a fabricar una
caja sin tapa, para
ello se recortaran
cuatro cuadrados,
uno en cada esquina
y se doblara la pieza
resultante.
*PROBLEMA 1
¿ Cuánto deben
*PROBLEMA 2
Medir los cuadrados que se recortaran para que el
*PROBLEMA 3
volumen de la caja sea el máximo?
QUE ES LA DERIVADA
° En matemáticas, la derivada de una función es una medida de la rapidez con la
que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se
calcula como el límite de la rapidez de cambio media de la función en un cierto
intervalo, cuando el intervalo considerado para la variable independiente se toma
cada vez más pequeño.

2. Página 2
Problema de la caja 2
El problema de la caja N°1
Se dispones de una pieza rectangular de cartón que mide 40 x
30.


Con este material se va a fabricar una caja, sin tapa, para
ello se recortara cuatro cuadrados, uno en cada esquina del
rectángulo y se doblara la pieza resultante para formar la
caja.
¿ Cuánto deben de medir los cuadrados que se recortaran
para que el volumen de la caja sea el máximo?
Tabla de recortes de los cuadrados (largo x ancho x altura=volumen)
“ La juventud es
el momento de
estudiar la
sabiduría; la
vejez, el de
practicarlo.”

3. En la siguiente
grafica se muestran los diversos
volumen de la
caja según sea el
recorte de esta.
V = (40 –2x)(30-2x)x
(1200-80x-60x-4x2 )x
4x3-140x2 + 1200x
Y = 4x3-140x2 + 1200x
dy/dx=12x2 –280x +1200
Puntos máximos: 5.6574 máximo
Puntos mínimos :17.6759 mínimo
“La
educación no
cambia al
mundo,
cambia a las
personas que
cambiaran al
mundo”
La capacidad del volumen ira cambiando según sea la altura o
recorte que se le hagan a los cuadrados en los extremos.