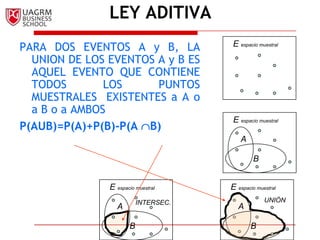
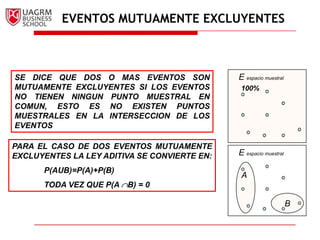
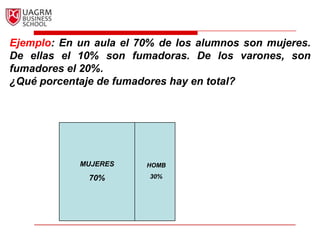
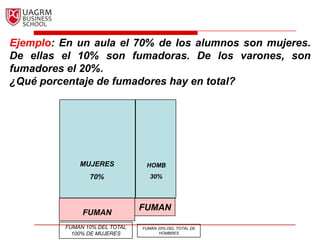
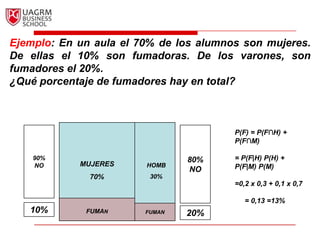
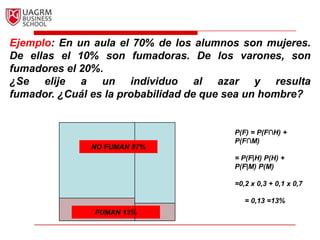
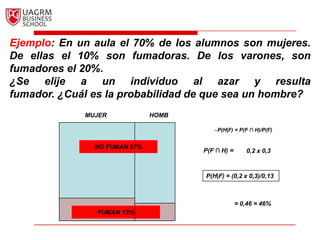
Este documento introduce los conceptos básicos de la probabilidad e inferencia estadística. Explica la noción de espacio muestral y eventos, y cómo se pueden asignar probabilidades numéricas a eventos usando diferentes métodos como el clásico, de frecuencia relativa o subjetivo. También cubre relaciones básicas como el complemento de un evento, la ley aditiva, eventos mutuamente excluyentes y probabilidad condicional.

1. PROBABILIDAD E INFERENCIA ESTADISTICAMaestría en banca valores y seguros( 2da Edición – 2da Versión )Msc Jorge Mario Jimenez Aviles10 de 2011Santa Cruz - Bolivia

2. INTRODUCCION A LA PROBABILIDADTEMA 5

3. INTRODUCCION A LA PROBABILIDADEl azar resulta en principio algo que engloba una serie de causas complejas que renunciamos a determinar y estudiar en detalles por difíciles de precisar, porque desconocemos

4. LA PROBABILIDAD CON MEDIDA NUMERICA DE LA POSIBILIDAD DE OCURRENCIAPOSIBILIDAD CRECIENTE DE OCURRENCIA100,5ProbabilidadLa ocurrencia del evento es igualmente probable que improbable

5. EXPERIMIENTOS Y EL ESPACIO MUESTRALCUANDO HAYAMOS DEFINIDO TODOS LOS RESULTADOS EXPERIMENTALES POSIBLES, HABREMOS IDENTIFICADO EL ESPACIO MUESTRA

6. Experimento aleatorioAquellos fenómenos con las siguientes propiedades:No se conoce a priori el resultadoSe conocen todos los resultados posibles.Se lo puede repetir bajo las mismas condiciones.

7. Espacio MuestralSe denomina al conjunto de todos los posibles resultados de un fenómeno aleatorio.Se lo nota con la letra S.Se tiran dos monedas:S= {(C,C);(C,+);(+,C);(+, +)}

8. EventosCada subconjunto del espacio muestral (del conjunto de resultados) se denomina evento. Si el evento consta de un solo elemento de S se lo denomina evento elemental o punto muestral. Si consta de más elementos recibe el nombre de evento compuesto.Sse lo llama evento seguroAl evento que no contiene ningún punto muestral se lo llama evento imposible (Ø).

9. Función de probabilidadPara una variable discreta es una función que cumple con:p(x)>=0Σx p(x)=1

10. Definición de probabilidadSupongamos tener un s con un numero finito de eventos simples, igualmente posibles.Llamaremos probabilidadde un evento A al cociente entre el número de eventos simples contenidos en A sobre el número total de eventos simples. P(A) =

11. METODOS PARA DETERMINAR PROBABILIDADESMETODO CLASICOMETODO DE FRECUENCIA RELATIVAMETODO SUBJETIVO

12. METODO CLASICO CUANDO COMO BASE PARA ASIGNAR LAS PROBABILIDADES SE UTILIZA LA SUPOSICION DE UN RESULTADO CON IGUAL POSIBILIDAD, EL PROCEDIMIENTO SE CONOCE COMO METODO CLASICO. EL METODO CLASICO ASIGNARA UNA PROBABILIDAD DE 1/n A CADA RESULTADO EXPERIMENTAL

13. EjemploConsideremos el experimento de arrojar dos dados:ESPACIO MUESTRAL

14. Sea el evento A={sacar un total de 8 puntos}.Numero de eventos simples que están contenidos en A: (6,2); (5,3); (4,4); (3,5);(2,6). Y el numero total de eventos elementales: 36.13.9%

15. Frecuencia relativaPodemos encarar entonces dos tipos de problemas:Cuando se conoce la probabilidad de un fenómeno, tenemos un valor guía de la frecuencia relativa que debemos esperar al aumentar el numero de experiencias.Cuando no conocemos la probabilidad, y la experiencia es grande, podemos tomar la frecuencia relativa como un valor aproximado de la probabilidad.

16. % FRECUENCIA LANZAR DOS DADOS

17. METODO SUBJETIVOMETODO CLASICO Y DE FRECUENCIA RELATIVA NO PUEDE APLICARSE EN TODAS LAS SITUACIONES DONDE SE DESEA ASIGNAR PROBABILIDADES

18. METODO SUBJETIVOEN EL METODO SUBJETIVO DE ASIGNAR PROBABILIDADES PODEMOS UTILIZAR CUALQUIER DATO DISPONIBLE ADEMAS DE NUESTRA EXPERIENCIA E INTUICIONDEBEN CUMPLIR: p(x)>=0 Σx p(x)=1

19. RELACIONES DE PROBABILIDAD BASICASCOMPLEMENTO DE UN EVENTO

20. LEY ADITIVAEVENTOS MUTUAMENTE EXCLUYENTESPROBABILIDAD CONDICIONALE espacio muestralE espacio muestralE espacio muestralAAA’COMPLEMENTO DE UN EVENTOPARA UN EVENTO A, EL COMPLEMENTO DEL EVENTO A ES AQUEL EVENTO QUE CONTIENE TODOS LOS PUNTOS MUESTRALES NO EXISTENTES EN A. EL COMPLEMENTO DE A SE IDENTIFICA COMO A’P(A’) = 1 - P(A)

21. E espacio muestralE espacio muestralE espacio muestralE espacio muestralAAABBUNIÓNBINTERSEC.LEY ADITIVAPARA DOS EVENTOS A y B, LA UNION DE LOS EVENTOS A y B ES AQUEL EVENTO QUE CONTIENE TODOS LOS PUNTOS MUESTRALES EXISTENTES a A o a B o a AMBOSP(AUB)=P(A)+P(B)-P(A B)

22. EVENTOS MUTUAMENTE EXCLUYENTESE espacio muestralE espacio muestral100%ABSE DICE QUE DOS O MAS EVENTOS SON MUTUAMENTE EXCLUYENTES SI LOS EVENTOS NO TIENEN NINGUN PUNTO MUESTRAL EN COMUN, ESTO ES NO EXISTEN PUNTOS MUESTRALES EN LA INTERSECCION DE LOS EVENTOS PARA EL CASO DE DOS EVENTOS MUTUAMENTE EXCLUYENTES LA LEY ADITIVA SE CONVIERTE EN: P(AUB)=P(A)+P(B) TODA VEZ QUE P(A B) = 0

23. PROBABILIDAD CONDICIONALLlamaremos probabilidad condicional P(B/A), a la probabilidad de B habiendo ocurrido A.

24. Como se sabe que A ha ocurrido, ella se vuelve el nuevo espacio muestral, reemplazando el S originalEjemplo: En un aula el 70% de los alumnos son mujeres. De ellas el 10% son fumadoras. De los varones, son fumadores el 20%.¿Qué porcentaje de fumadores hay en total?AULA

25. Ejemplo: En un aula el 70% de los alumnos son mujeres. De ellas el 10% son fumadoras. De los varones, son fumadores el 20%.¿Qué porcentaje de fumadores hay en total?MUJERES70%HOMB30%

26. Ejemplo: En un aula el 70% de los alumnos son mujeres. De ellas el 10% son fumadoras. De los varones, son fumadores el 20%.¿Qué porcentaje de fumadores hay en total?MUJERES70%HOMB30%FUMANFUMANFUMAN 10% DEL TOTAL 100% DE MUJERESFUMAN 20% DEL TOTAL DE HOMBRES

27. Ejemplo: En un aula el 70% de los alumnos son mujeres. De ellas el 10% son fumadoras. De los varones, son fumadores el 20%.¿Qué porcentaje de fumadores hay en total?90%NO80%NOP(F) = P(F∩H) + P(F∩M) = P(F|H) P(H) + P(F|M) P(M)=0,2 x 0,3 + 0,1 x 0,7 = 0,13 =13% MUJERES70%HOMB30%10%FUMANFUMAN20%

28. Ejemplo: En un aula el 70% de los alumnos son mujeres. De ellas el 10% son fumadoras. De los varones, son fumadores el 20%. ¿Se elije a un individuo al azar y resultafumador. ¿Cuál es la probabilidad de que sea un hombre?90%NO80%NOP(F) = P(F∩H) + P(F∩M) = P(F|H) P(H) + P(F|M) P(M)=0,2 x 0,3 + 0,1 x 0,7 = 0,13 =13% MUJERES70%HOMB30%10%FUMANFUMAN20%

29. Ejemplo: En un aula el 70% de los alumnos son mujeres. De ellas el 10% son fumadoras. De los varones, son fumadores el 20%. ¿Se elije a un individuo al azar y resultafumador. ¿Cuál es la probabilidad de que sea un hombre?P(F) = P(F∩H) + P(F∩M) = P(F|H) P(H) + P(F|M) P(M)=0,2 x 0,3 + 0,1 x 0,7 = 0,13 =13% NO FUMAN 87%FUMAN 13%

30. Ejemplo: En un aula el 70% de los alumnos son mujeres. De ellas el 10% son fumadoras. De los varones, son fumadores el 20%. ¿Se elije a un individuo al azar y resultafumador. ¿Cuál es la probabilidad de que sea un hombre?MUJERHOMBP(H|F) = P(F ∩ H)/P(F) NO FUMAN 87%P(F ∩ H) =0,2 x 0,3P(H|F) = (0,2 x 0,3)/0,13 = 0,46 = 46% FUMAN 13%

31. Expresión del problema en forma de arbolFumaP(F) = 0,7 x 0,1 + 0,3x0,20,1Mujer0,70,9No fumaP(H | F) = 0,3x0,2/P(F)EstudianteLos caminos a través de nodos representan intersecciones.

32. Las bifurcaciones representan uniones disjuntas.

33. Puedes resolver los problemasusando la técnica de tupreferencia.Fuma0,20,3Hombre0,8No fuma31

34. 32Nombre del Módulo dirección@deldocente.com

35. 33Nombre del Módulo dirección@deldocente.com