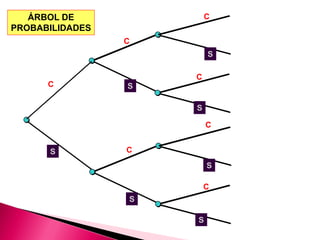
Este documento trata sobre conceptos básicos de probabilidad. Explica que la probabilidad es una medida numérica de la posibilidad de que un evento ocurra entre 0 y 1. También describe métodos para asignar valores de probabilidad como el método clásico y el método de frecuencia relativa. Finalmente, introduce conceptos como experimentos aleatorios, espacio muestral, eventos mutuamente excluyentes y no mutuamente excluyentes, y las reglas básicas de probabilidad.

1. PROBABILIDADES
Lic. MARIZA CARDENAS PINEDA

2. PROBABILIDAD
1 Cierto
 Es la medida
numérica de la
posibilidad de que un
.5
evento pueda ocurrir.
 Su valor está entre 0
y1 0 Imposible

3. ASIGNACION DE PROBABILIDADES
 En la asignación de probabilidades deben satisfacerse dos
requisitos básicos de probabilidades
i . Para cada resultado experimental Ei . 0 ≤ P(Ei) ≤ 1 , y
ii. P(E1) + P(E2) + … + P(En) = 1
► Métodos para asignar valores probabilísticos
♦ METODO CLASICO : Método de asignar probabilidades
basado en la hipótesis de que los resultados
experimentales son igualmente posibles
- Probabilidad a priori o probabilidad objetiva o lógica
- No será apropiada para tratar problemas económicos o
administrativos

4. 5-4
Enfoques de la probabilidad
 Probabilidad clásica: se basa en la
consideración de que los resultados de un
experimento son igualmente posibles.
 Utilizando el punto de vista clásico,
número de resultados favorables
Probabilidad de un evento =
número total de resultados posibles
Ejemplos:
Al lanzar un dado .¿Cuál es la probabilidad de que salga un número par?
En una baraja de cartas. ¿La probabilidad de que al extraer una carta
resulte una espada ?

5. ♦ METODO DE FRECUENCIA RELATIVA: es un método
de asignar probabilidades con base en la
experimentación o en datos históricos
- Probabilidad experimental, empírica o a posteriori
- Dado A :
P(A) = Nº. de veces que ocurrió A
Nº. total veces que se repitió experimento
♦ Se lanza un dado seis veces en cada ensayo, se observa
la frecuencia del número uno. Se han obtenido los
siguientes resultados: ENSAYOS Número
observados
de 1 Frecuencia
relativa
1 1 1/6
2 2 2/6
3 0 0/6
4 1 1/6
5 0 0/6
6 1
7 2
8 2
9 0

6. Frecuencia Relativa
1.00 Total de Caras
Número de Lanzamientos
0.75
0.50
0.25
0.00
0 25 50 75 100 125
Número de Lanzamientos

7. 5-10
Enfoques de la probabilidad
 Probabilidad Subjetiva: La probabilidad de
que suceda un evento específico que
asigna una persona con base en cualquier
información disponible.
- Probabilidad asignada bajo un criterio
personal, basado en cualquier tipo de
evidencia disponible
- Implica un grado de creencia personal
 Ejemplos de la probabilidad subjetiva son
estimar la probabilidad de que un equipo
de fútbol gane el campeonato este año.

8. Experimentos y Eventos
 ¿Cuál es la probabilidad de obtener 1 sello si
arrojamos una moneda una vez?
Número de Resultados Favorables
Prob 
Número de Resultados Posibles
s  1
 0.5
c, s 2

9. Experimentos y Eventos
 ¿Cuál es la probabilidad de obtener 1 cara si
arrojamos una moneda tres veces?
Número de Resultados Favorables
Prob 
Número de Resultados Posibles
(css), (scs), (ssc) 3
  0.375
(ccc ), (ccs ), (csc), (css), (scc), (scs), (ssc), (sss) 8

10. ÁRBOL DE C
PROBABILIDADES
C
S
C
C S
S
C
S C
S
C
S
S

11. Experimentos y Eventos
 ¿Si lanzamos 2 dados, cuál es la probabilidad
de obtener un puntaje de 7?
Número de Resultados Favorables
Prob 
Número de Resultados Posibles
(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)  6
 0.1667
62 36

12. Experimentos y Eventos
 ¿Cuál es la probabilidad de sacar un as al
sacar un naipe de una baraja?
Número de Resultados Favorables
Prob 
Número de Resultados Posibles
As de Corazones, As de Tréboles, As de Diamantes, As de Espadas  4

1
 0.0769
52 Naipes 52 13

13. Definiciones
 Experimento Aleatorio
◦ Actividad que origina un evento.
◦ Proceso de hacer una observación y obtener un
resultado.
 Evento
◦ Uno o más de los posibles resultados de un
experimento.
 Espacio Muestral
◦ Todos los posibles resultados de un experimento.
Diapositiva 13

14. Experimento aleatorio Espacio Muestral
Lanzar una moneda Cara, Sello.
Lanzar dos monedas CC, CS, SC, SS
Sacar una carta (valor) 2, 2, ..., A (52)
Sacar una carta (color) Roja, Negra
Lanzar un dado. 1, 2, 3, 4, 5, 6
Jugar un partido Ganar, Empatar,
Perder
Inspeccionar una producto Defectuoso, Bueno

15. Experimento: Lanzar dos monedas
Espacio Muestral: CC, CS, SC, SS
Evento Resultados
1 Cara y 1 Sello CS, SC
Cara en la 1ra. Moneda CC, CS
Al menos una Cara CC, CS, SC
Cara en cada lanzamiento CC

16. Clases de Eventos
 Eventos Mutuamente Excluyentes
◦ Dos o más eventos que no pueden ocurrir al
mismo tiempo.
◦ A: Reina de Corazones; B: Reina de Espadas
 Los eventos A y B son mutuamente
excluyentes.
 Eventos No Mutuamente Excluyentes
◦ Dos o más eventos que si pueden ocurrir al
mismo tiempo.
◦ A: Naipes de Corazones; B: As
 Los eventos A y B no son mutuamente
excluyentes.
 El As de Corazones
Diapositiva 16

17. Mutuamente Excluyentes
Evento A Evento B
Espacio Muestral

18. No Mutuamente Excluyentes
Evento A Evento B

19. AXIOMAS DE PROBABILIDAD
1. P(A) ≥ 0
2. P(Ω) = 1
Consecuencias
- 0 ≤ P(A) ≤ 1
- P(Φ) = 0 Probabilidad de un evento imposible
- P(AUA’) = P(A) + P(A’) = 1

20. PROBABILIDAD DE SUCESOS O EVENTOS
a). UN SUCESO PUEDE ESTAR CONTENIDO EN
OTRO: entonces, la probabilidad del primer
suceso será menor que la del suceso que lo
contiene.
Ejemplo: lanzamos un dado y analizamos dos sucesos:
a) Que salga el número 6, y
b) Que salga un número par.
Dijimos que el suceso a) está contenido en el suceso b).
P(A) = 1/6 = 0,166 P(B) = 3 / 6 = 0,50
Por lo tanto, podemos ver que la probabilidad
del suceso contenido.
suceso a), es menor que la probabilidad del
suceso que lo contiene, suceso b).

21. b). DOS SUCESOS PUEDEN SER IGUALES: en
este caso, las probabilidades de ambos sucesos
son las mismas.
Ejemplo: lanzamos un dado al aire y analizamos dos
sucesos: a) que salga número par, y b) que salga múltiplo
de 2. Las soluciones coinciden en ambos casos.
P(A) = 3 / 6 = 0,50
P(B) = 3 / 6 = 0,50

22. Ejemplo: lanzamos un dado al aire y
analizamos dos sucesos: a) que salga
número par, y b) que sea mayor que 3.
La intersección de estos dos sucesos tiene dos
elementos: el 4 y el 6.
Su probabilidad será por tanto:
P(A L B) = 2 / 6 = 0,33

23. Ejemplo: lanzamos un dado al aire y analizamos
dos sucesos: a) que salga número par, y b) que el
resultado sea mayor que 3.
El suceso unión estaría formado por los siguientes
resultados: el 2, el 4, el 5 y el 6.
P(A) = 3 / 6 = 0,50 P(B) = 3 / 6 = 0,50
P (A L B) = 2 / 6 = 0,33
Por lo tanto,
P (A u B) = (0,50 + 0,50) - 0,33 = 0,666

24. Ejemplo: lanzamos un dado al aire y analizamos
dos sucesos: a) que salga un número menor
que 3, y b) que salga el número 6.
La probabilidad del suceso unión de estos dos sucesos será igual a:
P(A) = 2 / 6 = 0,333
P(B) = 1 / 6 = 0,166
Por lo tanto:
P(A U B) = 0,33 + 0,166 = 0,50

25. P(B) = 1 - P(A)
Ejemplo: lanzamos un dado al aire. el suceso (A) es que
salga un número par, luego su complementario, suceso (B),
es que salga un número impar.
La probabilidad del suceso (A) es igual a :
P(A) = 3 / 6 = 0,50
Luego, la probabilidad del suceso (B) es igual a:
P(B) = 1 - P(A) = 1 - 0,50 = 0,50
Se puede comprobar aplicando la regla de "casos favorables /
casos posibles":
P(B) = 3 / 6 = 0,50

26. Ejemplo: seguimos con el ejemplo anterior: a) que
salga un número par, y b) que salga un número
impar.
La probabilidad del suceso unión de estos dos
sucesos será igual a:
P(A) = 3 / 6 = 0,50 P(B) = 3 / 6 = 0,50
Por lo tanto:
P(A U B) = 0,50 + 0,50 = 1

27. GRACIAS