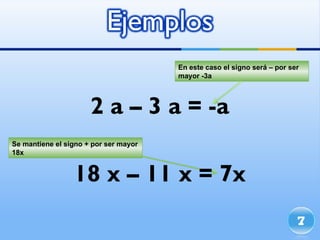
El documento explica los conceptos de términos semejantes, suma y resta de expresiones algebraicas. Indica que términos semejantes tienen la misma parte literal con iguales exponentes, y que al sumar o restar estos términos se juntan los coeficientes. También describe cómo realizar operaciones algebraicas como la suma y resta de polinomios, incluyendo la reducción de términos semejantes.

1. TÉRMINOS SEMEJANTES Sara Paola González Rosa Delia Originales 24 de Septiembre de 2011

2. Dos o más términos son semejantes cuando tienen la misma parte literal , o sea, cuando tienen iguales letras afectadas de iguales exponentes .

3. Ejemplos 2 a y a -2 b 8 b - a 8 b 4 -8 a 8 b 4 misma parte literal

4. Su objetivo es transformar en un solo término dos o más términos semejantes . En dicha reducción puede ocurrir los siguientes tres casos:

5. REGLA : Se suman los coeficientes poniendo delante de la suma el signo que tienen todos y después se escribe la parte literal.

6. Ejemplos 3 a + 2 a = 5 a -5 b – 7 b = -12 b - a 2 -9 ª 2 = -10 ª 2

8. 2 a – 3 a = -a 18 x – 11 x = 7x En este caso el signo será – por ser mayor -3a Se mantiene el signo + por ser mayor 18x

10. Ejemplos: Reducir: 5 a – 8 a + a - 6 a + 21 a Reducción de los positivos: 5 a + a + 21 a = 27 a Reducción de los negativos: -8 a -6 a = -14 a Se obtiene: 27 a – 14 a = 13 a

11. Es una operación que tiene por objeto reunir dos o más expresiones algebraicas (sumandos) en una sola expresión algebraica (suma) En Aritmética, la suma siempre significa aumento , pero en Algebra la suma es un concepto más general , pues puede significar aumento o disminución .

12. Para sumar dos o más expresiones algebraicas se escriben unas a continuación de las otras con sus propios signos y se reducen los términos semejantes si los hay.

13. Los siguientes ejemplos brindaran una mejor explicación de la suma: Ejemplo 1 Sumar 5a, 6b y 8c. 1. Los escribimos unos a continuación de otros con sus propios signos y como 5a=+5a, 6a=+6a, 8c=+8c.

14. Entonces la suma será: 5a + 6b + 8c. Por lo tanto será lo mismo sumar: 6b + 8c +5b NOTA : El orden de los sumandos no altera la suma

15. Ejemplo 2 Sumar 3a 2 b, 4a 2 b, a 2 b, 7ab 2 y 6b 3 La suma será: 3a 2 b + 4a 2 b + a 2 b + 7ab 2 + 6b 3

16. Como en esta expresión contamos con términos que no son semejantes tendremos que efectuar una reducción de los términos semejantes: 3 a 2 b + a 2 b = 4a 2 b 7ab 2 6b 3 El resultado será: 4a 2 b+ 7ab 2 + 6b 3 Términos semejantes No tenemos términos semejantes

17. La suma de polinomios suele indicarse incluyendo los sumandos dentro de paréntesis. Ejemplo 1 Sumar a-b, 2a+3b-c y -4a + 5b (a-b) + (2a+3b-c) + (-4ab + 5b)

18. (a-b) + (2a+3b-c) + (-4a + 5b) Como existen términos semejantes en la expresión, se deberán colocar unos debajo de los otros para así poder realizar la reducción de términos. a – b 2a + 3b – c -4a + 5b -a + 7b – c

19. Es una operación que tiene por objeto, dada una suma de dos sumandos (minuendos) y uno de ellos (sustraendo) , hallar el otro sumando (resta o diferencia). Es evidente, de esta definición, que la suma del sustraendo y la diferencia tiene que ser el minuendo

20. En Aritmética la resta siempre implica disminución , mientras que la resta algebraica tiene un carácter más general, pues puede significar disminución o aumento

21. Se escribe el minuendo con sus propios signos y a continuación el sustraendo con los signos cambiados y se reducen los términos semejantes, si los hay

22. Ejemplo 1 De -4 restar 7. Escribimos el minuendo con su propio signo que en este caso será -4. A continuación escribimos el sustraendo 7 con el signo cambiado

23. El resultado será: -4 – 7= -11 En efecto -11 es la diferencia porque sumada con el sustraendo 7 reproduce el minuendo -4: En la expresión aparece como +7 pero al momento de realizar la operación se cambia el signo que en este caso será -7

24. Cuando el sustraendo es un polinomio, hay que restar del minuendo cada uno de los términos del sustraendo, así que a continuación del minuendo se escribirá el sustraendo cambiándole el signo a todos sus términos

25. Ejemplo 1 De 4x – 3y + z restar 2x + 5z -6 1. En la sustracción indica incluyendo el sustraendo en un paréntesis precedido del signo menos 4x – 3y + z – (2x + 5z -6)

26. 2. Ahora se dejará el minuendo con sus propios signos y a continuación se escribirá el sustraendo cambiando el signo a todos los términos : 4x – 3y + z – 2x - 5z +6

27. Se reducirán todos los términos semejantes para obtener el resultado 4x – 3y + z -2x - 5z + 6 4x - 3y -4z + 6