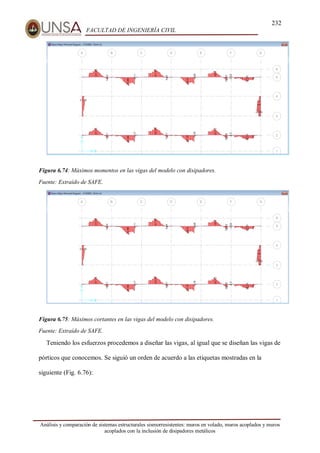
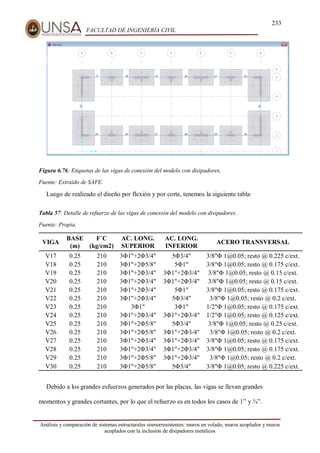
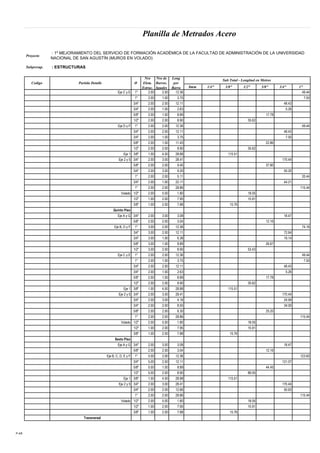
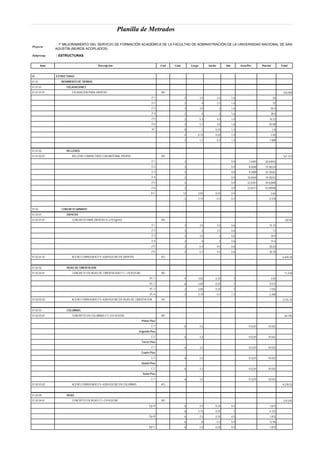
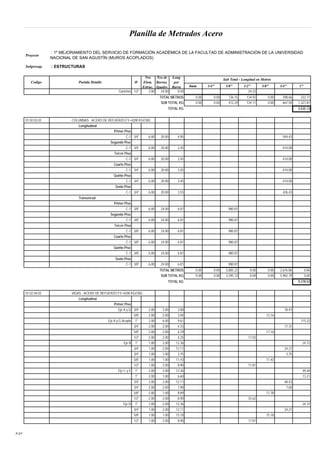
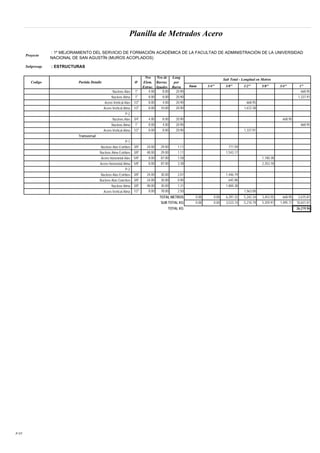
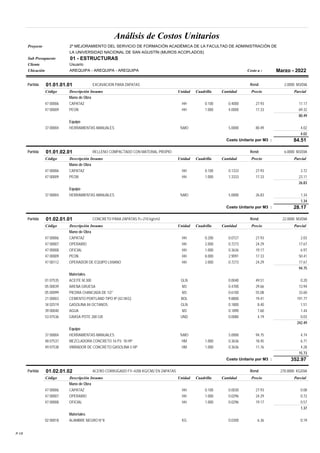
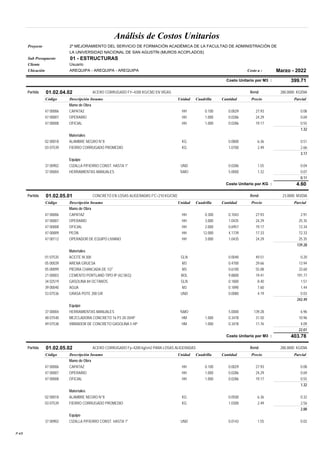
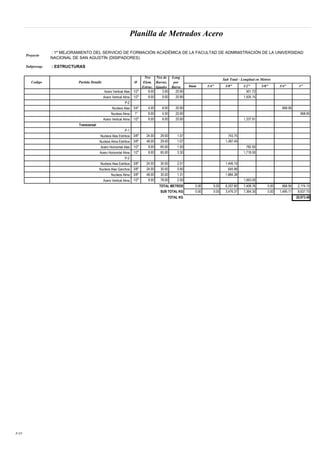
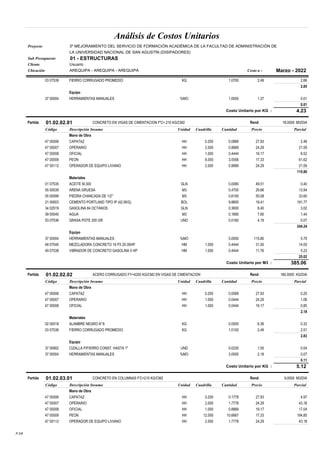
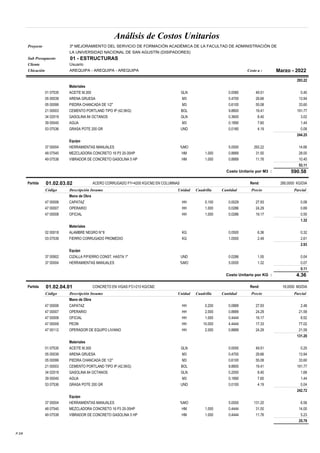
Este documento presenta un análisis y comparación de sistemas estructurales sismorresistentes para un edificio, incluyendo muros en volado, muros acoplados y muros acoplados con disipadores metálicos. Se realiza un modelo del edificio y un análisis sísmico lineal para los sistemas sin protección. Luego, se incluyen disipadores ADAS y TADAS en un análisis no lineal, evaluando parámetros como derivas, cortantes y energía disipada. El objetivo