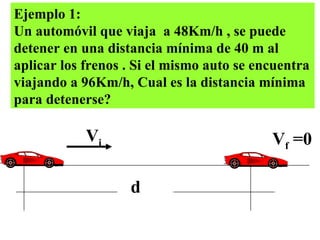
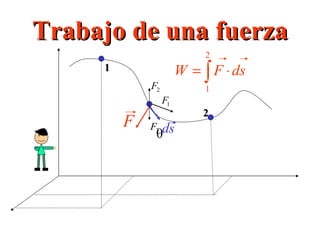
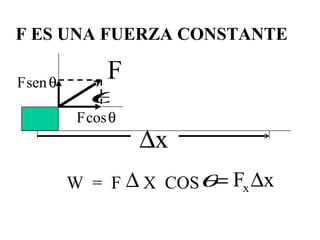
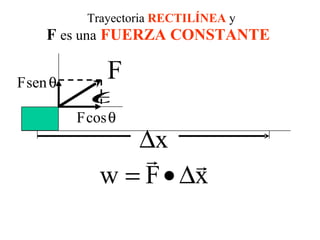
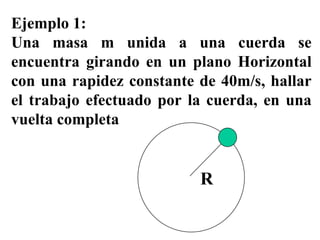
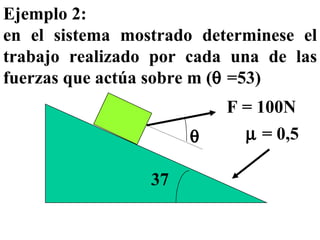
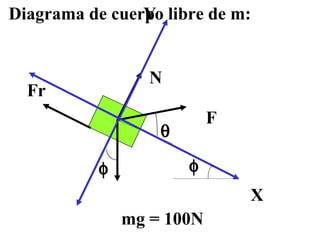
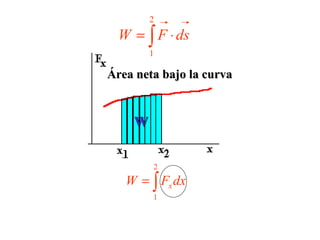
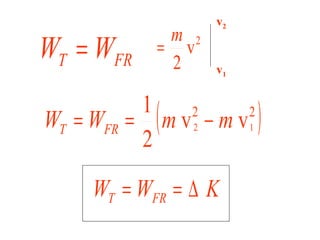El documento habla sobre conceptos de trabajo, energía y potencia en mecánica. Explica que el trabajo es la transferencia de energía mediante una fuerza y se define como el producto escalar de la fuerza y el desplazamiento. También describe cómo calcular el trabajo realizado por fuerzas constantes y variables, y introduce la relación entre trabajo y cambios en la energía cinética de un cuerpo según el teorema del trabajo y la energía.

1. Trabajo y energía

2. C 5 TRABAJO Y ENERGÍA MECÁNICA Trabajo de una fuerza constante y de una fuerza variable. Teorema del trabajo y la energía cinética. Potencia. Sears, Física Universitaria

3. ¿ Físicamente en qué se diferencian o asemejan ambas realizaciones? V 0 = 0 V = 0 V 0 = 0  t = s / V V = 0  t = h / V

4. Energía Medida cuantitativa del movimiento en todas sus formas.

5. Trabajo Medida cuantitativa de la transferencia de movimiento ordenado de un cuerpo a otro mediante la acción de una fuerza Cambio de posición, desplazamiento Relación geométrica entre el desplazamiento y la fuerza

6. Trabajo de una fuerza 1 2

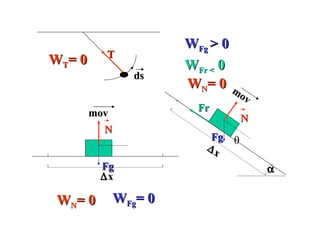
7. En los tramos donde cita < 9 0 o el trabajo es motor En los tramos donde cita > 9 0 o el trabajo es resistivo En los tramos en que cita = 90 el trabajo es nulo El trabajo es un escalar Escalar [J]

8. Trabajo realizado por una fuerza constantee

9. X 1 X2 X ¿CUÁL SERA EL TRABAJO EFECTUADO POR LA FUERZA F? F X = X 2 - X 1

10. Fuerza constante y desplazamiento rectilíneo mov  x F

11. F ES UNA FUERZA CONSTANTE W = F X COS

12. Trayectoria RECTILÍNEA y F es una FUERZA CONSTANTE

13. EL TRABAJO REALIZADO POR UNA FUERZA CONSTANTE ES IGUAL AL PRODUCTO DE LA COMPONENTE DE LA FUERZA A LO LARGO DE LA DIRECCION DEL DESPLAZAMIENTO POR EL DESPLAZAMIENTO EL TRABAJO REALIZADO POR UNA FUERZA CONSTANTE ES IGUAL AL PRODUCTO ESCALAR DEL VECTOR FUERZA POR EL DEZPLAZAMIENTO

14. X 1 X 2 W X(m)

15. EN TODA GRAFICA FUERZA vs DESPLAZAMIENTO EL AREA BAJO LA CURVA NOS DA ELTRABAJO REALIZADO POR LA FUERZA PARALELA AL DEZPLAZAMIENTO

16.  0 <  <  /2 Como Entonces el trabajo es positivo cos  > 0 F  X

17.  =  /2 Como Entonces las fuerzas perpendiculares al desplazamiento no realizan trabajo cos  = 0 F  X

18.   /2 <  <  Como Entonces el trabajo es negativo cos  <0 F  X

19. T ds W T = 0 W N = 0 mov  x N Fg W Fg = 0 W Fr < 0 Fr mov  x  Fg W Fg > 0 N W N = 0

20. Ejemplo 1: Una masa m unida a una cuerda se encuentra girando en un plano Horizontal con una rapidez constante de 40m/s, hallar el trabajo efectuado por la cuerda, en una vuelta completa R

21. Ejemplo 2: en el sistema mostrado determinese el trabajo realizado por cada una de las fuerzas que actúa sobre m (  =53) 37  F = 100N  = 0,5

22. F Diagrama de cuerpo libre de m: mg = 100N N Fr   Y X 

23. FUERZA VARIABLE , Desplazamiento rectilíneo F F x W = F x X i i i

24. Área neta bajo la curva W

25. Un cuerpo se mueve desde x= 0 hasta x = 6, bajo la acción de una fuerza tal como se indica , hallar el trabajo realizado 5 6 X(m) F x (N)

26. Expresión general para el trabajo F r C F : Fuerza C : trayectoria

27. Esta es la llamada integral de línea W =  F.dr =  ( F x dx +F y dy + F z dz) donde:F x , F y , F z : componentes de F y además la curva C está definida a través de: y =f(x), z =f(x) C C El trabajo efectuado por F cuando el cuerpo se mueve a través de la curva C esta dada por la expresión :

28. En sistema mostrado determínese el trabajo efectuado por la fuerza a a través del camino a) C1 b) C2 y x 10 5

29. El trabajo es una magnitud aditiva 1 2 C F i F R © © ©

30. Problema Se arrastra una caja por un piso áspero aplicando una fuerza constante de magnitud 50N. La fuerza forma un ángulo de 37 o arriba de la horizontal . Una fuerza de rozamiento de 10 N retarda el movimiento y la caja se desplaza una distancia de 3m hacia la derecha a) calculese el trabajo realizado por F b) el trabajo realizado por la fricción c) el trabajo, neto efectuado sobre la caja por todas las fuerzas que actúan sobre ella

31. Problema Una partícula que se mueve en el plano xy experimenta un desplazamiento: s = ( 2 i +3 j ) [m] según una trayectoria rectilínea. Mientras que una fuerza constante dada por F = ( 5 i +3 j ) [N] actúa sobre ella. a) calcúlese la magnitud el desplazamiento y de la fuerza b) el trabajo realizado por F c) el ángulo que la fuerza forma con el desplazamiento

32. Potencia: trabajo realizado por una fuerza, por unidad de tiempo [W] Se define como el trabajo efectuado por unidad de tiempo P =  W/  t : Potencia Promedio P = lim   W/  t = dW/dt   t  0 dW = F.dr entonces la potencia instantánea también se puede expresar como: P = F.dr/dt = F.V Donde V es la velocidad instantánea

33. Problema: Un elevador tiene una masa de 1000Kg y lleva una carga de 800Kg. Una fuerza de rozamiento constante de 4000N retarda su movimiento hacia arriba. a) cual debe ser la potencia que debe entregar el motor para levantar el elevador a una rapidez constante de 3m/s? b) que potencia debe entregar el motor en cualquier instante para proporcionar una aceleración hacia arriba de 1m/s 2 ?

34. Motor T Mg f

35. Teorema del W y la Energía cinética © © © © © v 1 v 2

36. v 1 v 2

37. Se define la energía cinética como : K= mV 2 /2 C omo la energía asociada al Movimiento mecánico de un cuerpo, luego: E l trabajo efectuado por la fuerza resultante o el trabajo total es igual al cambio en la energía cinética de la particula

38. Ejemplo 1: Un automóvil que viaja a 48Km/h , se puede detener en una distancia mínima de 40 m al aplicar los frenos . Si el mismo auto se encuentra viajando a 96Km/h, Cual es la distancia mínima para detenerse? V i d V f =0