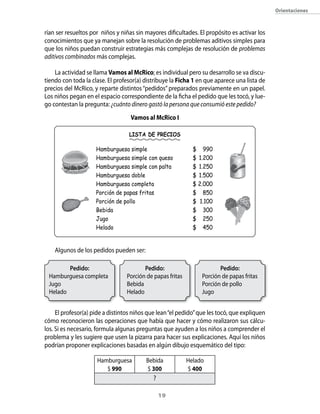
Este documento presenta una unidad didáctica sobre la resolución de problemas aditivos combinados para tercer año básico. La unidad se enfoca en que los estudiantes desarrollen estrategias para identificar las operaciones necesarias para resolver problemas que involucran más de una operación aritmética. Incluye orientaciones para los docentes sobre tareas matemáticas, variables didácticas, procedimientos y fundamentos centrales relacionados con la suma, resta y resolución de problemas aditivos.