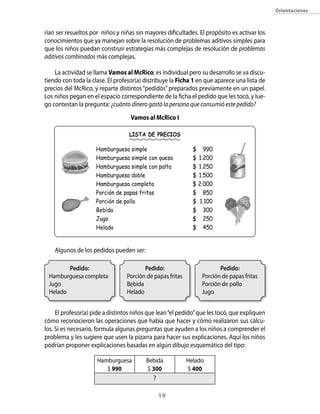
Este documento presenta una guía didáctica para la tercera unidad de matemáticas de tercero básico sobre problemas aditivos simples y combinados. La unidad busca que los estudiantes desarrollen estrategias para resolver problemas aditivos que incluyan identificar las operaciones necesarias. También se enfoca en técnicas para calcular sumas y restas como descomposiciones numéricas. La guía incluye aprendizajes esperados, tareas matemáticas, variables didácticas, procedimientos y fundamentos centrales de la un