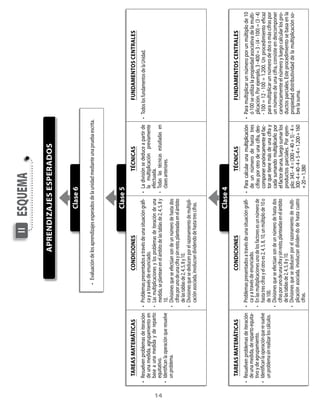
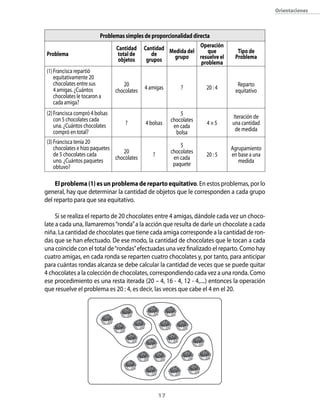
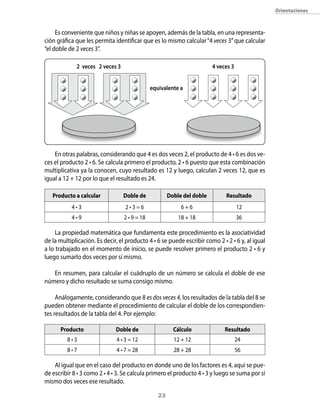
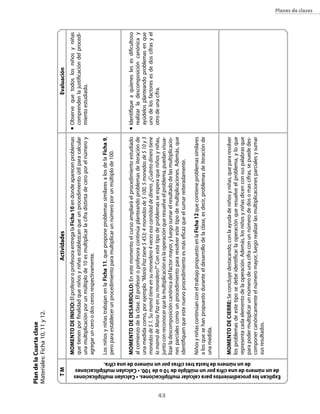
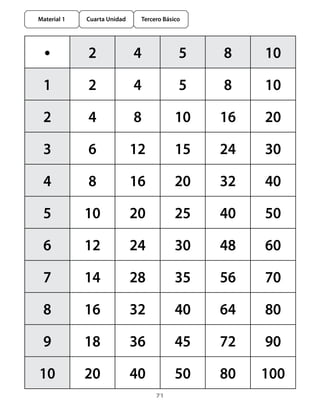
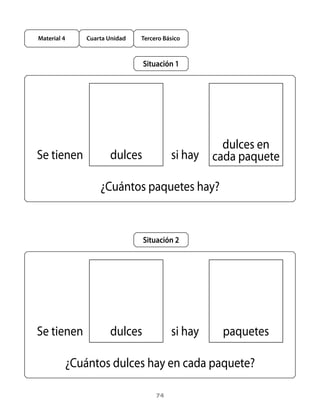
Este documento presenta una guía didáctica para la cuarta unidad de matemáticas de tercero básico sobre problemas multiplicativos y técnicas para multiplicar. La unidad se enfoca en resolver problemas que involucran multiplicación y división, ampliar el significado de estas operaciones, y desarrollar habilidades para calcular multiplicaciones y divisiones. La guía incluye aprendizajes esperados, tareas matemáticas, variables didácticas y procedimientos que los estudiantes deben construir.