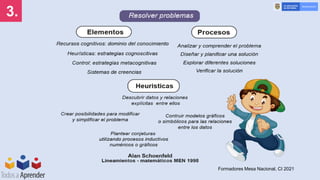
El documento presenta un enfoque sobre la mejora de prácticas pedagógicas en el pensamiento numérico a través de estrategias metacognitivas en la resolución de problemas. Se establecen objetivos generales y específicos sobre la identificación de estrategias, la creación de ambientes de aprendizaje y el fortalecimiento del conocimiento didáctico del docente. Además, se detallan etapas para el desarrollo de competencias y se proponen ejercicios prácticos que facilitan la enseñanza y evaluación del pensamiento numérico.