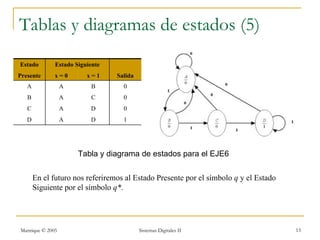
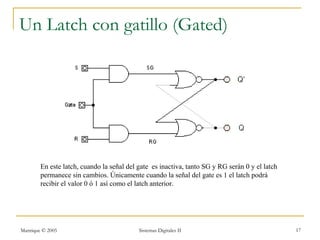
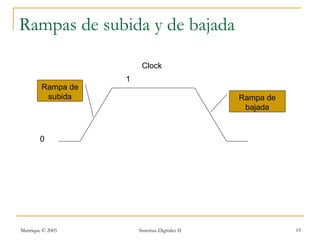
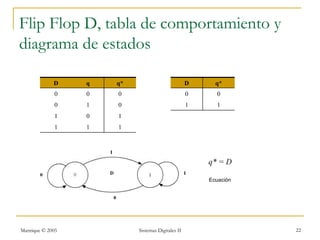
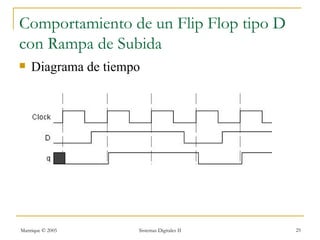
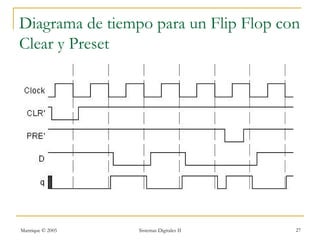
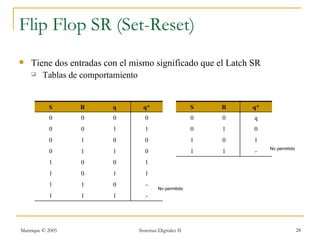
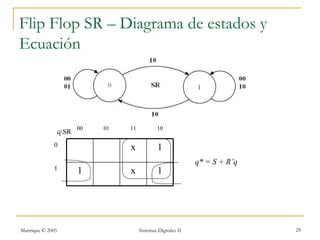
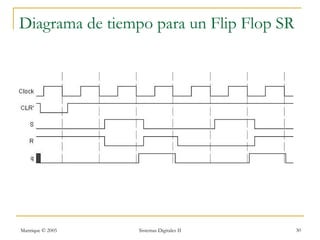
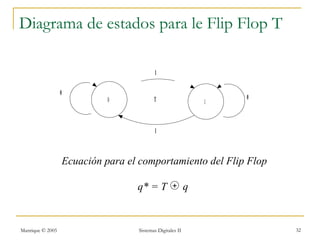
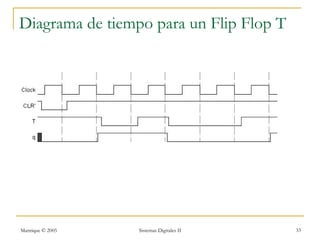
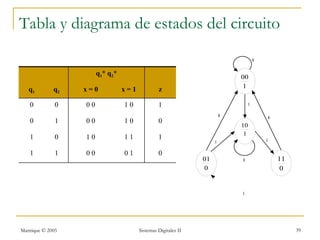
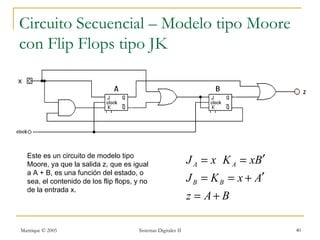
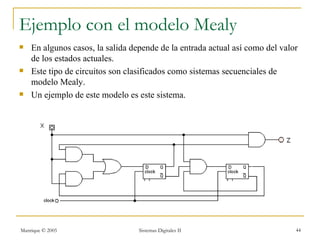
Este documento introduce los sistemas secuenciales o máquinas de estado finito, cuyas salidas dependen no solo de las entradas actuales sino también de estados pasados. Describe elementos de memoria como latches y flip-flops así como diferentes tipos de flip-flops como D, JK, SR y T. Explica cómo representar el comportamiento de sistemas secuenciales usando tablas de estados, diagramas de estados y rastreos temporales.