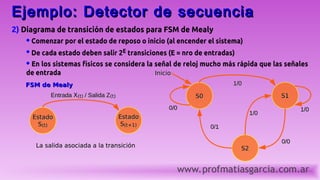
El documento describe los conceptos básicos de los autómatas y máquinas de estado finito. Explica que los autómatas son sistemas secuenciales síncronos que pueden encontrarse en uno de un número finito de estados y que generan salidas en función de las entradas y el estado actual. También describe los dos tipos principales de autómatas, Mealy y Moore, y cómo se pueden implementar máquinas de estado finito utilizando biestables y circuitos combinacionales. Además, presenta una metodología paso a paso para dise