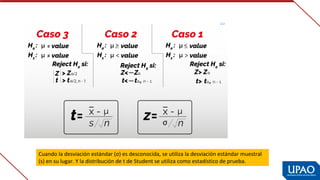
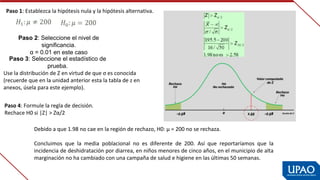
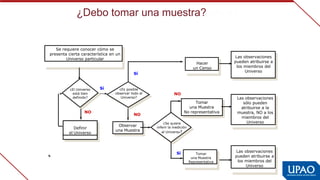
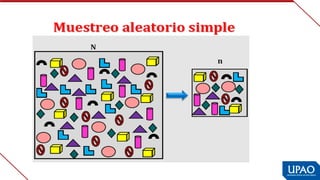
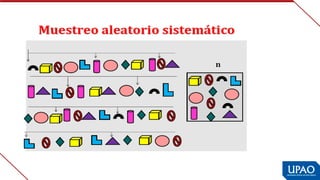
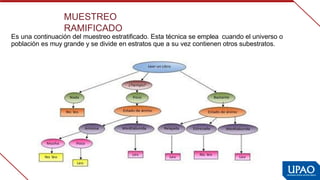
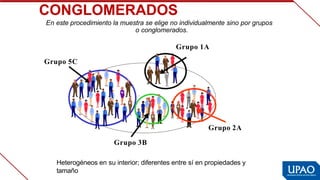
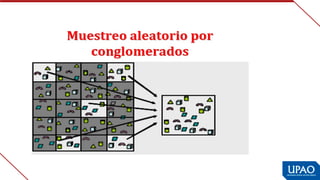
Este documento describe las variables de investigación, incluyendo su definición, clasificación y operacionalización. Explica que una variable es una característica o atributo que puede medirse o expresarse de diferentes maneras en los sujetos de un estudio. Luego clasifica las variables según su naturaleza (cuantitativas/cualitativas), complejidad (simples/complejas), nivel de medición (nominal, ordinal, de intervalo, de razón) y función (independiente, dependiente, interviniente, confusora). Finalmente, define la operacionaliz