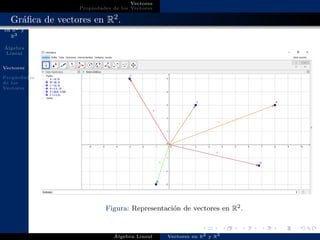
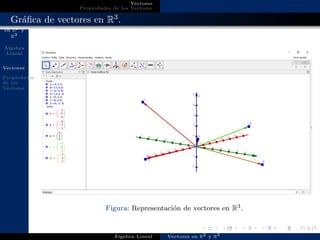
Este documento introduce los vectores en R2 y R3. Define un vector como un conjunto ordenado de números y explica que la notación indica el espacio donde se encuentra el vector. Describe cómo representar gráficamente vectores en R2 y R3 y enumera algunas propiedades de los vectores como la suma, el producto por escalar y el producto punto y cruz entre vectores.

1. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
´Algebra Lineal Vectores en R2 y R3

2. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
Vectores en R2 y R3
Braian Moreno Cifuentes
Departamento de Matem´aticas, F´ısica y Estad´ıstica
Universidad de La Sabana
´Algebra Lineal Vectores en R2 y R3

3. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
En esta presentaci´on, se introduce al estudiante la definici´on de vectores
en R2
y R3
dando sus propiedades, representaci´on gr´afica y algunos usos.
´Algebra Lineal Vectores en R2 y R3

4. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
¿Qu´e es un vector?
Definici´on
Un vector de n componentes se define como un conjunto ordenado de n
n´umeros escritos de la siguiente forma:
v = (x1, x2, x3, · · · , xn) Notaci´on por filas.
v =







x1
x2
x3
...
xn







Notaci´on por columnas.
La notaci´on de los vectores se hace por medio de letras min´usculas (por
ejemplo u, v, a, b, w) y la cantidad de n´umeros indica en qu´e espacio est´a
el vector.
´Algebra Lineal Vectores en R2 y R3

5. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
¿Qu´e es un vector?
Si v = (x1, x2, x3, · · · , xn), entoces se dice que v es un vector de n
componentes (ubicado en Rn
); adem´as x1 es la primera componente de v,
x2 es la segunda componente de v, y as´ı sucesivamente. En general, kk es
la k-´esima componente de v para todo k; 1 ≤ k ≤ n.
Ejemplo
El vector u = (4, 9, −6, 12) es un vector de 4 componentes y el valor −6 es
la tercera componente de u.
Ejemplo
El vector h = (−3, −16, 8, 4, −7, −8) es un vector de 6 componentes y el
valor −7 es la quinta componente de h.
Nota
Los vectores tienen representaci´on gr´afica s´olo en R, R2
y R3
. No es
posible representar un vector en un espacio m´as grande.
´Algebra Lineal Vectores en R2 y R3

6. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
Gr´afica de vectores en R2.
Figura: Representaci´on de vectores en R2.
´Algebra Lineal Vectores en R2 y R3

7. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
Gr´afica de vectores en R3.
Figura: Representaci´on de vectores en R3.
´Algebra Lineal Vectores en R2 y R3

8. Vectores
en R2 y
R3
´Algebra
Lineal
Vectores
Propiedades
de los
Vectores
Vectores
Propiedades de los Vectores
Propiedades de los vectores.
Definici´on
Sean u, v y w dos vectores en Rn
y α, β dos escalares. Entonces se define:
• Suma de vectores. u + v =
(u1, u2, · · · , un)+(v1, v2, · · · , vn) = (u1 +v1, u2 +v2, · · · , un +vn) ∈ Rn
.
• Producto por escalar. αu = α(u1, u2, · · · , un) = (αu1, αu2, · · · , αun).
• Producto punto
u · v=(u1, u2, · · · , un) · (v1, v2, · · · , vn) = u1v1 + u2 + v2 + · · · + unvn=
k ∈ R.
• Producto cruz. Sean u y v dos vectores definidos en R3
. Entonces,
u × vest´a dado por:
u × v =
i j k
u1 u2 u3
v1 v2 v3
= i
u2 u3
v2 v3
− j
u1 u3
v1 v3
+ k
u1 u2
v1 v2
= l ∈ R3
´Algebra Lineal Vectores en R2 y R3