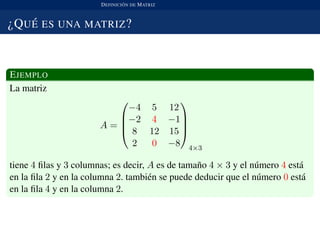
El documento aborda el concepto de matrices, incluyendo su definición, notación y tipos, como matrices cuadradas, triangulares, identidad, transpuestas y simétricas. Además, se explican las operaciones básicas entre matrices, como la suma y el producto, destacando sus definiciones, requisitos y ejemplos. Se enfatiza la importancia de realizar ejercicios diarios para dominar el manejo de matrices.

2. MATRICES Y PROPIEDADES
Braian Moreno Cifuentes
Departamento de Matem´aticas, f´ısica y Estad´ıstica
Universidad de La Sabana

3. En esta presentaci´on se busca contextualizar al estudiante con respecto al con-
cepto de matriz, como armar una matriz, identificar posiciones de elementos y
revisar como se hacen operaciones entre matrices.

4. DEFINICI ´ON DE MATRIZ
¿QU ´E ES UNA MATRIZ?
DEFINICI ´ON
Una matriz es un arreglo rectangular de mn n´umeros dispuestos en m filas
(renglones) y n columnas.
NOTA
Las matrices se representan por medio de letras may´usculas (A, B, C), y en la
mayor´ıa de los casos, las entradas (los n´umero que forman a la matriz) son
n´umeros pertenecientes a los reales {aij ∈ R; 1 ≤ i ≤ m; 1 ≤ j ≤ n}.

5. DEFINICI ´ON DE MATRIZ
¿QU ´E ES UNA MATRIZ?
La notaci´on de una matriz A de tama˜no m × n es:
A =







a11 a12 a13 · · · a1n
a21 a22 a23 · · · a2n
a31 a32 a33 · · · a3n
...
...
...
...
...
am1 am2 am3 · · · amn







m×n
Donde m × n muestra el tama˜no de la matriz tratada y cada uno de las
entradas (n´umeros) aij con 1 ≤ i ≤ m y 1 ≤ j ≤ n representa la posici´on en
la matriz.

6. DEFINICI ´ON DE MATRIZ
¿QU ´E ES UNA MATRIZ?
EJEMPLO
La matriz
A =




−4 5 12
−2 4 −1
8 12 15
2 0 −8




4×3
tiene 4 filas y 3 columnas; es decir, A es de tama˜no 4 × 3 y el n´umero 4 est´a
en la fila 2 y en la columna 2. tambi´en se puede deducir que el n´umero 0 est´a
en la fila 4 y en la columna 2.

7. TIPOS DE MATRICES
ALGUNOS TIPOS DE MATRICES
MATRIZ CUADRADA
El n´umero de filas y columnas es el mismo.
B =


2 4 3
−8 6 8
4 −6 12


3×3
es una matriz cuadrada ya que es de tama˜no 3 × 3.

8. TIPOS DE MATRICES
ALGUNOS TIPOS DE MATRICES
MATRIZ TRIANGULAR SUPERIOR
Matriz donde todas las entradas debajo de la diagonal principal son 0.
U =




1 2 4 5
0 −2 4 −7
0 0 12 81
0 0 0 16




4×4
V =


3 3 6 7 −2
0 2 7 12 4
0 0 8 44 43


3×5
Donde los n´umeros en rojo forman la diagonal principal de las matrices U y
V . No es necesario que la matriz sea cuadrada.

9. TIPOS DE MATRICES
ALGUNOS TIPOS DE MATRICES
MATRIZ TRIANGULAR INFERIOR
Matriz donde todas las entradas encima de la diagonal principal son 0.
L =




1 0 0 0
3 −2 0 0
4 0 12 0
6 10 3 16




4×4
P =


3 0 0 0 0
10 2 0 0 0
20 32 8 0 0


3×5
Donde los n´umeros en rojo forman la diagonal principal de las matrices L y
P. No es necesario que la matriz sea cuadrada.

10. TIPOS DE MATRICES
ALGUNOS TIPOS DE MATRICES
MATRIZ IDENTIDAD
Matriz donde todos los elementos encima y debajo de la diagonal principal
son 0. Adem´as, la diagonal principal est´a formada con entradas 1.
I3 =


1 0 0
0 1 0
0 0 1


3×3

11. TIPOS DE MATRICES
ALGUNOS TIPOS DE MATRICES
MATRIZ TRANSPUESTA
Matriz donde se intercambian las filas por las columnas y viceversa. No es
necesario que la matriz sea cuadrada.
A =
6 7 8 12
4 8 −9 3 2×4
AT =




6 4
7 8
8 −9
12 3




4×2
MATRIZ SIM ´ETRICA
Matriz donde se intercambian las filas por las columnas y viceversa resultando
la mista matriz.
A =


1 2 3
2 8 −9
3 −9 5


3×3
AT =


1 2 3
2 8 −9
3 −9 5


3×3

12. TIPOS DE MATRICES
ALGUNOS TIPOS DE MATRICES
Existen otros tipos de matrices como:
Matriz idempotente.
Matriz de Valdermonde.
Matriz de Valores Propios.
Matriz semejante.
Que ser´an estudiadas a lo largo del curso.

13. OPERACIONES ENTRE MATRICES
Una vez se conozca la forma de construir matrices, se hace necesario aprender
a hacer operaciones entre matrices, ya que la idea es entender la matriz como
un arreglo que puede ser operada con otras matrices de su mismo tipo.
Es as´ı como se introducen los conceptos de suma de matrices y de producto
matricial para ver la forma de operaci´on de ´estas.

14. OPERACIONES ENTRE MATRICES SUMA DE MATRICES
SUMA DE MATRICES
DEFINICI ´ON
Sean A y B dos matrices de tama˜no m × n. La suma de A y B, notada por
A + B est´a dada por:
A + B =
=



a11 a12 a13 · · · a1n
a21 a22 a23 · · · a2n
a31 a32 a33 · · · a3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
am1 am2 am3 · · · amn



m×n
+



b11 b12 b13 · · · b1n
b21 b22 b23 · · · b2n
b31 b32 b33 · · · b3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
bm1 bm2 bm3 · · · bmn



m×n
=



a11 + b11 a12 + b12 a13 + b13 · · · a1n + b1n
a21 + b21 a22 + b22 a23 + b23 · · · a2n + b2n
a31 + b31 a32 + b32 a33 + b33 · · · a3n + b3n
.
.
.
.
.
.
.
.
.
..
.
.
.
.
am1 + bm1 am2 + bm2 am3 + bm3 · · · amn + bmn



m×n

15. OPERACIONES ENTRE MATRICES SUMA DE MATRICES
PARA TENER EN CUENTA
NOTA
Es importante tener en cuenta que solo se puede efectuar suma de matrices s´ı
y s´olo s´ı son del mismo tama˜no. Por ejemplo, A2×3 + B2×3 = (A + B)2×3;
mientra que A2×3 + B3×2 no se pueden sumar.

16. OPERACIONES ENTRE MATRICES SUMA DE MATRICES
EJEMPLO
EJEMPLO DE SUMA
Sean
A =
1 2 3
4 7 −2 2×3
B =
−4 −6 7
2 10 7 2×3
La suma A + B est´a dada por:
A + B =
1 2 3
4 7 −2 2×3
+
−4 −6 7
2 10 7 2×3
=
−3 −4 10
6 17 5 2×3

17. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
PRODUCTOS
A diferencia de los n´umeros reales, las matrices tienen dos tipos de productos:
El producto por escalar y el producto matricial. Se debe tener en cuenta que
ambos son totalmente diferentes.

18. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
PRODUCTO POR ESCALAR
Es el primero de los dos productos y consiste en multiplicar todas las entradas
de la matriz por un mismo n´umero (llamado escalar).
DEFINICI ´ON
Sea A una matriz de m × n y α un escalar. El producto del escalar α por la
matriz A, notado por αA est´a dado por:
αA = α



a11 a12 a13 · · · a1n
a21 a22 a23 · · · a2n
a31 a32 a33 · · · a3n
.
.
.
.
.
.
.
.
.
..
.
.
.
.
am1 am2 am3 · · · amn



m×n
=



αa11 αa12 αa13 · · · αa1n
αa21 αa22 αa23 · · · αa2n
αa31 αa32 αa33 · · · αa3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
αam1 αam2 αam3 · · · αamn



m×n

19. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
OBSERVACI ´ON
NOTA
El producto por escalar se puede hacer para cualquier matriz, sin restricci´on
con respecto al tama˜no.

20. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
EJEMPLO
EJEMPLO PRODUCTO POR ESCALAR
Sea
A =
12 −7 8 5
4 5 −9 12
1 −2 3 −4
12 21 12 0 4×4
Si α = 2, entonces 2A es igual a:
A =
24 −14 16 10
8 10 −18 24
2 −4 6 −8
24 42 24 0 4×4
De igual forma, si α = −3, entonces −3A es igual a:
A =
−36 21 −24 −15
−12 −15 27 −36
−3 6 −9 12
−36 −63 −36 0 4×4

21. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
PRODUCTO MATRICIAL
Es otra operaci´on definida entre matrices que, como se ver´a en la definici´on,
es totalmente diferente a la forma de multiplicar dos n´umeros reales. Es aqu´ı
donde aparece cierta dificultad a la hora de operar.
DEFINICI ´ON
Sea A una matriz de m × n y B una matriz de n × m. El producto matricial
de A y B, notado por AB est´a dado por:
AB =



a11 a12 a13 · · · a1n
a21 a22 a23 · · · a2n
a31 a32 a33 · · · a3n
.
.
.
.
.
.
.
.
.
..
.
.
.
.
am1 am2 am3 · · · amn



m×n



b11 b12 b13 · · · b1m
b21 b22 b23 · · · b2m
b31 b32 b33 · · · b3m
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
bn1 bn2 bn3 · · · bnm



n×m
=
a11b11 + a12b21 + · · · + a1nbn1 · · · a11b1m + a12b2m + · · · + a1nbnm
.
.
.
.
.
.
.
.
.
am1b11 + am2b21 + · · · + amnbn1 · · · am1b1m + am2b2m + · · · + amnbnm
m×m

22. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
OBSERVACI ´ON
Al inicio, el producto matricial resulta algo complicado de realizar por la
cantidad de cuentas que se deben hacer.
NOTA
El producto matricial NO ES CONMUTATIVO; es decir, AB = BA. Es ac´a
donde se presenta la diferencia entre operar n´umeros reales y operar matrices.

23. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
EJEMPLO
EJEMPLO PRODUCTO MATRICIAL
Sean
A =
12 5 7
−4 8 −3 2×3
B =


3 0
8 −1
−5 7


3×2
El producto matricial AB est´a dado por:
AB =
12 5 7
−4 8 −3 2×3


3 0
8 −1
−5 7


3×2
= (12 ∗ 3) + (5 ∗ 8) + (7 ∗ (−5)) (12 ∗ 0) + (5 ∗ (−1)) + (7 ∗ 7)
((−4) ∗ 3) + (8 ∗ 8) + ((−3) ∗ (−5)) ((−4) ∗ 0) + (8 ∗ (−1)) + ((−3) ∗ 7)
=
41 44
67 −29 2×2

24. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
EJEMPLO
EJEMPLO PRODUCTO MATRICIAL
Sean
A =
12 5 7
−4 8 −3 2×3
B =


3 0
8 −1
−5 7


3×2
El producto matricial BA est´a dado por:
BA =


3 0
8 −1
−5 7


3×2
12 5 7
−4 8 −3 2×3
=
(3 ∗ 12) + (0 ∗ (−4)) (3 ∗ 5) + (0 ∗ 8) (3 ∗ 7) + (0 ∗ (−3))
(8 ∗ 12) + ((−1) ∗ (−4)) (8 ∗ 5) + ((−1) ∗ 8) (8 ∗ 7) + ((−1) ∗ (−3))
((−5) ∗ 12) + (7 ∗ (−4)) ((−5) ∗ 5) + (7 ∗ 8) ((−5) ∗ 7) + (7 ∗ (−3))
=


36 15 21
100 32 59
−88 31 −56



25. OPERACIONES ENTRE MATRICES PRODUCTO ENTRE MATRICES
PARA TENER EN CUENTA
NOTA
Una forma ´util de concluir si se puede hacer el producto matricial es observar
que el n´umero de columnas de la primera matriz a multiplicar es igual al
n´umer de filas de la segunda matriz a multiplicar. El resultado final es una
matriz con el tama˜no de filas correspondiente a la primera matriz por las
columnas de la segunda matriz.
NOTA
Es importante tener en cuenta que la forma m´as sencilla de hacer operaciones
entre matrices es realizando ejercicios a diario para comprender y
”mecanizar”las cuentas hechas en cada una de ellas.