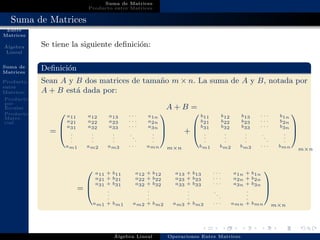
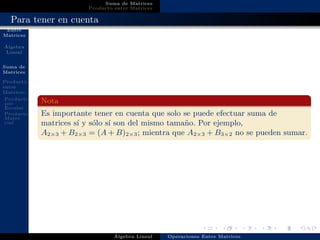
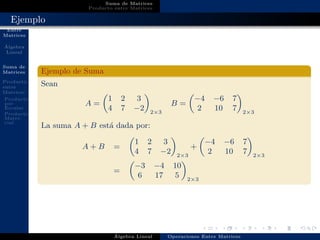
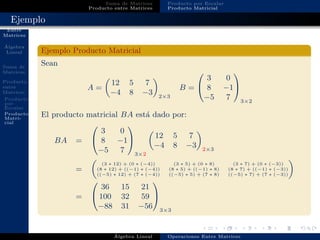
Este documento define las principales operaciones entre matrices, incluyendo la suma, el producto por escalar y el producto matricial. Explica que la suma de matrices involucra sumar los elementos correspondientes siempre que las matrices sean del mismo tamaño, mientras que el producto por escalar multiplica cada elemento de la matriz por un escalar. Finalmente, el producto matricial es diferente a la multiplicación de números reales y requiere multiplicar las filas de una matriz por las columnas de otra.

1. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
´Algebra Lineal Operaciones Entre Matrices

2. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Operaciones Entre Matrices
Braian Moreno Cifuentes
Departamento de Matem´aticas, F´ısica y Estad´ıstica
Universidad de La Sabana
´Algebra Lineal Operaciones Entre Matrices

3. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
En esta presentaci´on, se definen las operaciones b´asicas entre matrices,
como lo son la suma, el producto por escalar y el producto matricial
mostrando algunos ejemplos.
´Algebra Lineal Operaciones Entre Matrices

4. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Suma de Matrices
Se tiene la siguiente definici´on:
Definici´on
Sean A y B dos matrices de tama˜no m × n. La suma de A y B, notada por
A + B est´a dada por:
A + B =
=



a11 a12 a13 · · · a1n
a21 a22 a23 · · · a2n
a31 a32 a33 · · · a3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
am1 am2 am3 · · · amn



m×n
+



b11 b12 b13 · · · b1n
b21 b22 b23 · · · b2n
b31 b32 b33 · · · b3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
bm1 bm2 bm3 · · · bmn



m×n
=



a11 + b11 a12 + b12 a13 + b13 · · · a1n + b1n
a21 + b21 a22 + b22 a23 + b23 · · · a2n + b2n
a31 + b31 a32 + b32 a33 + b33 · · · a3n + b3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
am1 + bm1 am2 + bm2 am3 + bm3 · · · amn + bmn



m×n
´Algebra Lineal Operaciones Entre Matrices

5. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Para tener en cuenta
Nota
Es importante tener en cuenta que solo se puede efectuar suma de
matrices s´ı y s´olo s´ı son del mismo tama˜no. Por ejemplo,
A2×3 + B2×3 = (A + B)2×3; mientra que A2×3 + B3×2 no se pueden sumar.
´Algebra Lineal Operaciones Entre Matrices

6. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Ejemplo
Ejemplo de Suma
Sean
A =
1 2 3
4 7 −2 2×3
B =
−4 −6 7
2 10 7 2×3
La suma A + B est´a dada por:
A + B =
1 2 3
4 7 −2 2×3
+
−4 −6 7
2 10 7 2×3
=
−3 −4 10
6 17 5 2×3
´Algebra Lineal Operaciones Entre Matrices

7. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Productos
A diferencia de los n´umeros reales, las matrices tienen dos tipos de
productos: El producto por escalar y el producto matricial. Se debe tener
en cuenta que ambos son totalmente diferentes.
´Algebra Lineal Operaciones Entre Matrices

8. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Producto por Escalar
Es el primero de los dos productos y consiste en multiplicar todas las
entradas de la matriz por un mismo n´umero (llamado escalar).
Definici´on
Sea A una matriz de m × n y α un escalar. El producto del escalar α por
la matriz A, notado por αA est´a dado por:
αA = α







a11 a12 a13 · · · a1n
a21 a22 a23 · · · a2n
a31 a32 a33 · · · a3n
...
...
...
...
...
am1 am2 am3 · · · amn







m×n
=







αa11 αa12 αa13 · · · αa1n
αa21 αa22 αa23 · · · αa2n
αa31 αa32 αa33 · · · αa3n
...
...
...
...
...
αam1 αam2 αam3 · · · αamn







m×n
´Algebra Lineal Operaciones Entre Matrices

9. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Observaci´on
Nota
El producto por escalar se puede hacer para cualquier matriz, sin
restricci´on con respecto al tama˜no.
´Algebra Lineal Operaciones Entre Matrices

10. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Ejemplo
Ejemplo Producto por Escalar
Sea
A =
12 −7 8 5
4 5 −9 12
1 −2 3 −4
12 21 12 0
4×4
Si α = 2, entonces 2A es igual a:
A =
24 −14 16 10
8 10 −18 24
2 −4 6 −8
24 42 24 0
4×4
De igual forma, si α = −3, entonces −3A es igual a:
A =
−36 21 −24 −15
−12 −15 27 −36
−3 6 −9 12
−36 −63 −36 0
4×4
´Algebra Lineal Operaciones Entre Matrices

11. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Producto Matricial
Es otra operaci´on definida entre matrices que, como se ver´a en la
definici´on, es totalmente diferente a la forma de multiplicar dos n´umeros
reales. Es aqu´ı donde aparece cierta dificultad a la hora de operar.
Definici´on
Sea A una matriz de m × n y B una matriz de n × m. El producto
matricial de A y B, notado por AB est´a dado por:
AB =



a11 a12 a13 · · · a1n
a21 a22 a23 · · · a2n
a31 a32 a33 · · · a3n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
am1 am2 am3 · · · amn



m×n



b11 b12 b13 · · · b1m
b21 b22 b23 · · · b2m
b31 b32 b33 · · · b3m
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
bn1 bn2 bn3 · · · bnm



n×m
=
a11b11 + a12b21 + · · · + a1nbn1 · · · a11b1m + a12b2m + · · · + a1nbnm
.
.
.
.
.
.
.
.
.
am1b11 + am2b21 + · · · + amnbn1 · · · am1b1m + am2b2m + · · · + amnbnm m×m
´Algebra Lineal Operaciones Entre Matrices

12. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Observaci´on
Al inicio, el producto matricial resulta algo complicado de realizar por la
cantidad de cuentas que se deben hacer.
Nota
El producto matricial NO ES CONMUTATIVO; es decir, AB = BA.
Es ac´a donde se presenta la diferencia entre operar n´umeros reales y
operar matrices.
´Algebra Lineal Operaciones Entre Matrices

13. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Ejemplo
Ejemplo Producto Matricial
Sean
A =
12 5 7
−4 8 −3 2×3
B =


3 0
8 −1
−5 7


3×2
El producto matricial AB est´a dado por:
AB =
12 5 7
−4 8 −3 2×3


3 0
8 −1
−5 7


3×2
= (12 ∗ 3) + (5 ∗ 8) + (7 ∗ (−5)) (12 ∗ 0) + (5 ∗ (−1)) + (7 ∗ 7)
((−4) ∗ 3) + (8 ∗ 8) + ((−3) ∗ (−5)) ((−4) ∗ 0) + (8 ∗ (−1)) + ((−3) ∗ 7)
=
41 44
67 −29 2×2
´Algebra Lineal Operaciones Entre Matrices

14. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Ejemplo
Ejemplo Producto Matricial
Sean
A =
12 5 7
−4 8 −3 2×3
B =


3 0
8 −1
−5 7


3×2
El producto matricial BA est´a dado por:
BA =


3 0
8 −1
−5 7


3×2
12 5 7
−4 8 −3 2×3
=
(3 ∗ 12) + (0 ∗ (−4)) (3 ∗ 5) + (0 ∗ 8) (3 ∗ 7) + (0 ∗ (−3))
(8 ∗ 12) + ((−1) ∗ (−4)) (8 ∗ 5) + ((−1) ∗ 8) (8 ∗ 7) + ((−1) ∗ (−3))
((−5) ∗ 12) + (7 ∗ (−4)) ((−5) ∗ 5) + (7 ∗ 8) ((−5) ∗ 7) + (7 ∗ (−3))
=


36 15 21
100 32 59
−88 31 −56


3×3
´Algebra Lineal Operaciones Entre Matrices

15. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Para Tener en Cuenta
Nota
Una forma ´util de concluir si se puede hacer el producto matricial es
observar que el n´umero de columnas de la primera matriz a multiplicar es
igual al n´umer de filas de la segunda matriz a multiplicar. El resultado
final es una matriz con el tama˜no de filas correspondiente a la primera
matriz por las columnas de la segunda matriz.
Nota
Es importante tener en cuenta que la forma m´as sencilla de hacer
operaciones entre matrices es realizando ejercicios a diario para
comprender y ”mecanizar”las cuentas hechas en cada una de ellas.
´Algebra Lineal Operaciones Entre Matrices

16. Operaciones
Entre
Matrices
´Algebra
Lineal
Suma de
Matrices
Producto
entre
Matrices
Producto
por
Escalar
Producto
Matri-
cial
Suma de Matrices
Producto entre Matrices
Producto por Escalar
Producto Matricial
Comentario Final
El producto matricial se realizar al aplicar un concepto llamado producto
punto que ser´a tratado en la parte de operaciones entre vectores. Por
ahora, es importante tener claridad de como son las operaciones existentes
entre las matrices.
´Algebra Lineal Operaciones Entre Matrices