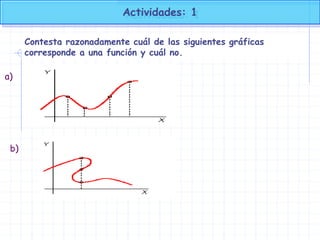
1. Actividades: 1
Contesta razonadamente cuál de las siguientes gráficas
corresponde a una función y cuál no.
a)
b)

2. Actividades: 1
Contesta razonadamente cuál de las siguientes gráficas
corresponde a una función y cuál no.
a)
b)
Si es una función, porque
cada x tiene un solo valor
de y
No es una función, porque
algunas x tienen varios
valores de y

3. Actividades: 2
Estas gráficas responden, en otro orden, a las situaciones que aparecen
debajo de ellas. Relaciona cada gráfica con la situación que refleja.
1 ALTURA DE UNA PELOTA QUE BOTA, AL PASAR EL TIEMPO.
2 NIVEL DE RUIDO DE UNA CALLE DESDE LAS 6 DE LA MAÑANA HASTA LAS 6 DE LA TARDE.
3 TEMPERATURAS MÍNIMAS DIARIAS EN TOLEDO, A LO LARGO DE UN AÑO.
4 PRECIO DE LAS BOLSAS DE PATATAS FRITAS.
5 NIVEL DE AGUA EN UN PANTANO A LO LARGO DEL AÑO.
6 DISTANCIA A LA TIERRA DE UN SATÉLITE ARTIFICIAL, AL PASAR EL TIEMPO.

4. Actividades: 2
4 PRECIO DE LAS BOLSAS DE PATATAS FRITAS
1 ALTURA DE UNA PELOTA QUE BOTA,AL PASAR EL TIEMPO.
3 TEMPERATURAS MÍNIMAS DIARIAS EN TOLEDO,A LO LARGO DE UN AÑO.
2 NIVEL DE RUIDO DE UNA CALLE DESDE LAS 6 DE LA MAÑANA HASTA LAS 6
DE LA TARDE
5 NIVEL DE AGUA EN UN PANTANO A LO LARGO DEL AÑO
6 DISTANCIA A LA TIERRA DE UN SATÉLITE ARTIFICIAL, AL PASAR EL
TIEMPO

5. Actividades: 3
Estas gráficas responden, en otro orden, a las situaciones que aparecen
debajo de ellas. Relaciona cada gráfica con la situación que refleja y di, en
cada caso, qué representan sus ejes de abscisas(EJE X) y ordenadas/EJE Y).
1) ALTURA DE UNA PELOTA QUE BOTA, AL PASAR EL TIEMPO.
2) NIVEL DE RUIDO DE UNA CALLE DESDE LAS 6 DE LA MAÑANA HASTA LAS 6 DE LA
TARDE.
3) TEMPERATURAS MÍNIMAS DIARIAS EN TOLEDO, A LO LARGO DE UN AÑO.
4) PRECIO DE LAS BOLSAS DE PATATAS FRITAS.
5) NIVEL DE AGUA EN UN PANTANO A LO LARGO DEL AÑO.
6) DISTANCIA A LA TIERRA DE UN SATÉLITE ARTIFICIAL, AL PASAR EL TIEMPO.

6. Actividades: 3
4 PRECIO DE LAS BOLSAS DE PATATAS FRITAS
1 ALTURA DE UNA PELOTA QUE BOTA,AL PASAR EL
TIEMPO.
3 TEMPERATURAS MÍNIMAS DIARIAS EN TOLEDO,A LO
LARGO DE UN AÑO.
2 NIVEL DE RUIDO DE UNA CALLE DESDE LAS 6 DE LA
MAÑANA HASTA LAS 6 DE LA TARDE
5 NIVEL DE AGUA EN UN PANTANO A LO LARGO DEL AÑO
6 DISTANCIA A LA TIERRA DE UN SATÉLITE ARTIFICIAL, AL
PASAR EL TIEMPO
Eje Y:
Precio
Eje X: Nº de bolsas de patatas fritas
Eje Y:
Altura
Eje X: Tiempo
Eje X: Días del año
Eje Y:
Temperaturas
mínimas
Eje Y: Nivel
de ruido
Eje X: Horas del día
Eje Y:
Distancia
Eje X: Tiempo
Eje Y:Nivel
de agua
Eje X: Meses del
año

7. Actividades: 4
Di cual es el dominio y el recorrido de las siguientes funciones

8. Actividades: 4
Aquí no hay gráfica
Aquí no hay gráfica
Aquí
no hay
gráfica
Aquí
no hay
gráfica
Dominio: [ 0, 9]
Recorrido:
[0, 8]
Aquí
no hay
gráfica
Aquí
no hay
gráfica
Aquí no hay gráfica
Aquí no hay gráfica
Dominio: [ 0, 9]
Recorrido:
[0, 7]
Aquí
no hay
gráfica
Aquí
no hay
gráfica
Aquí
no hay
gráfica
Aquí
no hay
gráfica
Aquí no hay gráfica
Aquí no hay gráfica
Aquí no hay gráfica
Aquí no hay gráfica
Dominio: [ 0, 8] Dominio: [ 0, 8]
Recorrido:
[0, 6]
Recorrido:
[0, 8]

9. Actividades: 5
Sea un globo que se eleva y, al alcanzar cierta altura, estalla.La siguiente
gráfica representa la altura, con el paso del tiempo, a la que se encuentra
el globo hasta que estalla.
a) ¿A qué altura estalla? ¿Cuánto tarda en estallar desde que lo
soltamos?
b) ¿Qué variables intervienen? ¿Qué escala se utiliza para cada
variable? ¿Cuál es el dominio de definición de esta función?
c) ¿Qué altura gana el globo entre el minuto 0 y el 4? ¿Y entre el 4 y
el 8? ¿En cuál de estos dos intervalos crece más rápidamente la
función?

10. Actividades: 5
a) ¿A qué altura estalla?
A 500 metros
¿Cuánto tarda en estallar desde que lo soltamos?
12 minutos

11. Actividades: 5
b) ¿Qué variables intervienen?
Eje X (variable independiente) : Tiempo
Eje y (variable dependiente) : Altura
¿Qué escala se utiliza para cada variable?
Eje X: cada cuadrito representa 1 minuto. Escala 1 : 1
Eje Y: cada cuadrito representa 50 metros. Escala 1 : 50
¿Cuál es el dominio de definición de esta función?
La gráfica empieza a los 0 minutos y acaba a los 12 minutos, cuando el
globo estalla, entonces...
Dominio [ 0, 12]

12. Actividades: 5
c) ¿Qué altura gana el globo entre el minuto 0 y el 4?
Aproximadamente, 250 metros
¿Y entre el 4 y el 8?
Aproximadamente, 400-250=150 metros
¿En cuál de estos dos intervalos crece más rápidamente la función?
En el primer intervalo, entre el minuto 0 y el 4. Intervalo [0, 4]

13. Actividades: 6
a) ¿Cuáles de las siguientes gráficas corresponden a una función continua?
b) ¿Cuáles de las siguientes gráficas corresponden a una función discontinua?

14. Actividades: 6
No es continua Si es continua

15. Actividades: 7
En la puerta de un colegio hay un puesto de
golosinas. En esta gráfica se ve la cantidad de
dinero que hay en su caja a lo largo de un día.
¿Es esta una función continua o discontinua?

16. Actividades: 7
¿Es esta una función continua o discontinua?
De 14 a 15 horas, el puesto se cierra, por eso no hay gráfica.
Entonces, es una función discontinua
Aquí está
cerrado

17. Actividades: 8
a)¿Cuál de estas gráficas es decreciente?
b)¿Cuál de estas gráfica es creciente?
c)¿Cuál de estas gráficas es a veces creciente y a veces no? ¿Dónde?
d) ¿Hay alguna que sea constante en alguna parte de su dominio?
a) c)b)

18. Actividades: 8
a)¿Cuál de estas gráficas es decreciente? La B
b)¿Cuál de estas gráfica es creciente? La C
c)¿Cuál de estas gráficas es a veces creciente y a veces no? ¿Dónde?
La gráfica A. Es creciente en el intervalo [ 0, 60 ] y luego es constante
en el resto de su dominio
d) ¿Hay alguna que sea constante en alguna parte de su dominio?
Si, la gráfica A es constante en el intervalo [ 60, 80]
a) c)b)
Aquí es
creciente

19. Actividades: 9
En la puerta de un colegio hay un puesto de golosinas. En esta gráfica
se ve la cantidad de dinero que hay en su caja a lo largo de un día.
a) ¿A qué hora empiezan las clases de la mañana?
b) ¿A qué hora es el recreo? ¿Cuánto dura?
c) El puesto se cierra a mediodía, y el dueño se lleva el dinero a casa. ¿Cuáles
fueron los ingresos esta mañana?
d) ¿Cuál es el horario de tarde en el colegio?

20. Actividades: 9
a) ¿A qué hora empiezan las clases de la mañana?
Fíjate que en los tramos que están señalados con las flechas, se
mantienen constantes los ingresos del puesto de caramelos. Como no hay
ventas, debe ser que los alumnos están en clase durante esas horas.
Teniendo en cuenta esto, las clases empiezan a las 8.30
b) ¿A qué hora es el recreo? ¿Cuánto dura?
El recreo empieza a las 11 y acaba a las 11.30. Dura media hora.

21. Actividades: 9
c) El puesto se cierra a mediodía, y el dueño se lleva el dinero a casa.
¿Cuáles fueron los ingresos esta mañana?
Fíjate que había 4 euros por la mañana cuando abrió el puesto.
Entonces, los ingresos de la mañana fueron: 22-4=18 euros.
d) ¿Cuál es el horario de tarde en el colegio?
Fíjate que de 15.30 a 17 horas la gráfica es constate, porque no hay
ventas.
Entonces el horario de tarde es de 15.30 a 17 horas
Aquí están
en clase

22. a)¿Cuál de estas gráficas es convexa?
b)¿Cuál de estas gráfica es cóncava?
c)¿Cuál de estas gráficas es a veces convexa y a veces cóncava ?
¿Dónde?
d)¿Cuál de estas gráficas no es ni cóncava ni convexa?
Actividades: 10
D
X
Y

23. a)¿Cuál de estas gráficas es convexa? La gráfica D
b)¿Cuál de estas gráfica es cóncava? La gráfica A
c)¿Cuál de estas gráficas es a veces convexa y a veces cóncava ?
¿Dónde? La gráfica C. Es convexa hasta 0 y cóncava después.
d)¿Cuál de estas gráficas no es ni cóncava ni convexa? La gráfica B
Actividades: 10
D
X
Y

24. Actividades: 11
a)Observa esta gráfica y di si tiene algún máximo?
b) ¿Y algún mínimo?

25. Actividades: 11
a)Observa esta gráfica y di si tiene algún máximo?
Si. Máximo: punto ( 6, 4 )
b) ¿Y algún mínimo?
Si. mínimo: punto ( 18, 0.5 )
Aquí hay un
Máximo
Aquí hay un
mínimo

26. Actividades: 12
Para medir la capacidad espiratoria de los pulmones, se hace una
prueba que consiste en inspirar al máximo y después espirar tan
rápido como se pueda en un aparato llamado “espirómetro”. Esta
curva indica el volumen de aire que entra y sale de los pulmones.
a) ¿Cuál es el volumen en el momento inicial?
b) ¿Cuánto tiempo duró la observación?
c) ¿Cuál es la capacidad máxima de los pulmones de esta persona?
d) ¿Cuál es el volumen a los 10 segundos de iniciarse la prueba?

27. Actividades: 12
a) ¿Cuál es el volumen en el momento inicial?
Es 1.5 litros
b) ¿Cuánto tiempo duró la observación?
Duró 18 segundos

28. Actividades: 12
c) ¿Cuál es la capacidad máxima de los pulmones de esta persona?
Es 4 litros
d) ¿Cuál es el volumen a los 10 segundos de iniciarse la prueba?
Es un litro
Aquí hay un
Máximo

29. Actividades: 13
Los cestillos de una noria van subiendo y bajando a medida que la
noria gira.
Esta es la representación gráfica de la función tiempo-distancia al
suelo de uno de los cestillos:
a) ¿Cuánto tarda en dar una vuelta completa?
b) Observa cuál es la altura máxima y di cuál es el radio de la noria.
c) Explica cómo calcular la altura a los 130 segundos sin necesidad de
continuar la gráfica.

30. Actividades: 13
a)¿Cuánto tarda en dar una vuelta completa?
Tarda 40 segundos
b) Observa cuál es la altura máxima y di cuál es el radio de la noria.
La altura máxima es 16 metros. El radio de la noria es, por tanto, 8
metros
Este es el periodo

31. Actividades: 13
c) Explica cómo calcular la altura a los 130 segundos sin necesidad de
continuar la gráfica.
Es una función periódica, luego a los 40 segundos, 80 segundos, 120
segundos, está abajo. Por tanto, a los 130 segundos está en la misma
posición que a los 10 segundos. Entonces a los 130 segundos está a 8 m
de altura.
Este es el periodo

32. Actividades: 14
a) ¿Cuál es su dominio de definición?
b) ¿Tiene máximo y mínimo? En caso afirmativo, ¿cuáles son?
c) ¿Cuáles son los puntos de corte con los ejes?
d) ¿Para qué valores de x es creciente y para cuáles es
decreciente?
Observa la gráfica de la función y responde:

33. Actividades: 14
a) ¿Cuál es su dominio de definición?
Dom f = R
b) ¿Tiene máximo y mínimo? En caso afirmativo, ¿cuáles son?
Máximo : (–2, 2) Mínimo : (0, –3)
c) ¿Cuáles son los puntos de corte con los ejes?
Con el eje X : (–4, 0), (3, 0), (–1, 0)
Con el eje Y : (0, –3)
d) ¿Para qué valores de x es creciente y para cuáles es
decreciente?
Creciente : (–8, –2) U (0, +8)
Decreciente : (–2, 0)

34. Actividades: 16
Relaciona cada gráfica con una de las expresiones analíticas:

35. Actividades: 16
Relaciona cada gráfica con una de las expresiones analíticas: