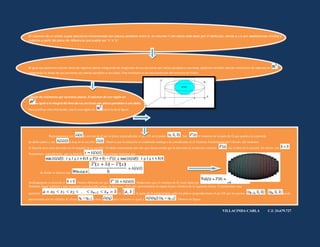
1. El volumen de un sólido cuyas secciones transversales son planos paralelos entre sí, el volumen V del sólido está dado por V=abA(x)dx, donde a y b son lasdistancias mínima y
máxima a partir del plano de referencia que puede ser “x” o “y”.
Al igual que podemos calcular áreas de regiones planas integrando las longitudes de sus secciones por rectas paralelas a una dada, podemos también calcular volúmenes de regiones en
integrando las áreas de sus secciones por planos paralelos a uno dado. Este resultado es un caso particular del teorema de Fubini.
Cálculo de volúmenes por secciones planas. El volumen de una región en
es igual a la integral del área de sus secciones por planos paralelos a uno dado.
Para justificar esta afirmación, sea Ω una región en como la de la figura.
Representemos por la sección de Ω por el plano perpendicular al eje OX en el punto . Sea el volumen de la parte de Ω que queda a la izquierda
de dicho plano y sea el área de la sección . Observa que la situación es totalmente análoga a la considerada en el Teorema Fundemental del Cálculo: allí teníamos
la función área cuya derivada era la longitud de la sección. No debe sorprenderte por ello que ahora resulte que la derivada de la función volumen, , sea el área de la sección. En efecto, sea .
Suponiendo, naturalmente, que la función es continua, tenemos que
,
de donde se deduce que
Análogamente se procede si . Hemos obtenido así que . Deducimos que el volumen de Ω viene dado por .
Podemos llegar también a este resultado considerando sumas de Riemann. Para ello aproximamos la región Ω por cilindros de la siguiente forma. Consideremos una
partición de ; la parte de Ω comprendida entre los planos perpendiculares al eje OX por los puntos y puede
aproximarse por un cilindro de altura y base cuyo volumen es igual a . Observa la figura.
VILLACINDA CARLA C.I: 24.679.727