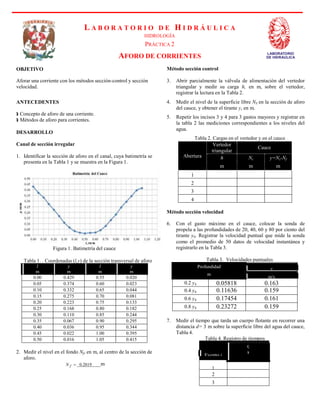
1. l
m
y
m
l
m
y
m
0.00 0.429 0.55 0.020
0.05 0.374 0.60 0.023
0.10 0.332 0.65 0.044
0.15 0.275 0.70 0.081
0.20 0.223 0.75 0.133
0.25 0.168 0.80 0.182
0.30 0.110 0.85 0.244
0.35 0.067 0.90 0.295
0.40 0.036 0.95 0.344
0.45 0.022 1.00 0.395
0.50 0.016 1.05 0.415
Profundidad v
m
m/s
0.2 y4 0.05818 0.163
0.4 y4 0.11636 0.159
0.6 y4 0.17454 0.161
0.8 y4 0.23272 0.159
ti
s
Evento i
1
2
3
OBJETIVO
L A B O R A T O R I O D E H I D R Á U L I C A
HIDROLOGÍA
PRÁCTICA 2
AFORO DE CORRIENTES
Método sección control
LABORATORIO
DE HIDRAULICA
Aforar una corriente con los métodos sección-control y sección
velocidad.
ANTECEDENTES
 Concepto de aforo de una corriente.
 Métodos de aforo para corrientes.
DESARROLLO
3. Abrir parcialmente la válvula de alimentación del vertedor
triangular y medir su carga h, en m, sobre el vertedor,
registrar la lectura en la Tabla 2.
4. Medir el nivel de la superficie libre NS en la sección de aforo
del cauce, y obtener el tirante y, en m.
5. Repetir los incisos 3 y 4 para 3 gastos mayores y registrar en
la tabla 2 las mediciones correspondientes a los niveles del
agua.
Canal de sección irregular
Tabla 2. Cargas en el vertedor y en el cauce
Vertedor
triangular
Cauce
1. Identificar la sección de aforo en el canal, cuya batimetría se
presenta en la Tabla 1 y se muestra en la Figura 1.
Abertura
1
2
3
4
h Ns y=Ns-Nf
m m m
Método sección velocidad
Figura 1. Batimetría del cauce
Tabla 1. . Coordenadas (l,y) de la sección transversal de aforo
6. Con el gasto máximo en el cauce, colocar la sonda de
propela a las profundidades de 20, 40, 60 y 80 por ciento del
tirante y4. Registrar la velocidad puntual que mide la sonda
como el promedio de 50 datos de velocidad instantánea y
registrarlo en la Tabla 3.
Tabla 3. Velocidades puntuales
7. Medir el tiempo que tarda un cuerpo flotante en recorrer una
distancia d= 3 m sobre la superficie libre del agua del cauce,
Tabla 4.
2. Medir el nivel en el fondo Nf, en m, al centro de la sección de
aforo.
Tabla 4. Registro de tiempos
N f   0.2819 m

2. 3
MEMORIA DE CÁLCULO
Método sección control
1. Calcular el gasto Q, en m3
/s, en el vertedor triangular, para
cada una de las cargas registradas en la Tabla 2.
Q  C h5/2
donde:
h carga sobre el vertedor, en m
C coeficiente de descarga del vertedor, en m1/2
/s
V 
1
v  v  v  v  v 
5
0.2y4 0.4y4 0.6y4 0.8y4 Sup
8. Dibujar un plano a escala que contenga:
a) La sección transversal de aforo, en color negro a partir de
los datos de la Tabla 1.
b) La superficie libre del agua en color azul, para el tirante
y4.
c) Indicar los puntos de medición de las velocidades con su
valor correspondiente, según la Tabla 3 y la superficial.
d) Especifique la escala utilizada.
C    2g tan

K 9. Determinar el área hidráulica A, en m2
, de la sección de
 8   
15   2 
aforo.
g aceleración de la gravedad, 9.81 en m/s2
 ángulo en el vértice del vertedor de aforo, 60°
 coeficiente experimental que depende de h y , según
la figura 7.9 de la referencia 1
K coeficiente que depende de B/h, según la figura 7.10 de
la referencia 1
B ancho del canal de aproximación B = 1.065 m
2. Presentar en una tabla los valores de gasto que corresponde a
cada tirante medido en el cauce, Tabla 5.
Tabla 5. Tirantes-gastos del río
Gasto del vertedor Tirantes en el río
Evento
m3
/s m
1 Q1 y1
2 Q2 y2
3 Q3 y3
4 Q4 y4
3. Obtener la ecuación de ajuste de la forma Q  ky n
para los
datos de la Tabla 5, empleando una regresión lineal simple.
Justificar el cálculo de las variables k y n.
4. Dibujar la curva Q-y con los puntos experimentales de la
Tabla 5.
5. En el mismo plano del punto 4, dibujar la curva Q-y ajustada
del punto 3 desde el origen.
Método sección-velocidad
6. Obtener la velocidad superficial como
10. Dibujar la curva de velocidades de la sección de aforo,
incluir las puntuales y la media.
Figura 2. Curva de velocidades teórica en un eje vertical de una
corriente.
11. Determinar el gasto QSV, en m3
/s, como
QSV = V A
12. Calcular el error relativo en porciento, entre los gastos Q4
correspondiente al método sección control y QSV
correspondiente al método sección velocidad.
Q  Q
v
d 3 1 e  4 SV 100
donde
Sup  
i1 ti
Q4
EQUIPO PARA LA EXPERIMENTACIÓN
ti tiempo en s, registrado en la tabla 4
d distancia de recorrido para el cuerpo flotante
7. Calcular la velocidad media V, en m/s, a partir del promedio
de las velocidades registradas en la tabla 3 y la velocidad
superficial del punto 6.
 Flexómetro
 Sonda electromagnética
 Cronómetro
 Flotador

3. REFERENCIAS BIBIOGRÁFICAS
1. Sotelo A. G. Hidráulica General Vol. 1, Ed. Limusa. México
1990.
2. Aparicio M. F. J. Fundamentos de Hidrología de Superficie,
Ed. Limusa. México, 1990.
3. Springal G. R., Hidrología Superficial, Ed. Limusa. México,
1990.
4. Chow, V. T. Hidrología aplicada, Ed. McGraw Hill.
México, 1994.
CUESTIONARIO
1.-¿Es posible emplear siempre el método sección control para el
aforo de una corriente?
2.- ¿Qué condiciones debe cumplir el tramo de un cauce para
instalar en éste una estación hidrométrica?
3.- ¿Qué instrumentos se emplean para determinar la elevación
de la superficie libre del agua en una estación hidrométrica?
4.-¿Para qué se emplea la curva elevaciones-gastos de un río?
5.-Si una avenida ocurrió en la noche y no fue posible
determinar en la estación de aforo el gasto, sino únicamente
quedó registrada la elevación máxima, ¿cómo se determinaría
el gasto?

4. Figura 3. Distribución de velocidades en río natural

5. ANTECEDENTES
Métodos de aforo para corrientes
AFORO VOLUMÉTRICO. Se aplica generalmente en los laboratorios de hidráulica, ya que solo es funcional para
pequeños caudales; sin embargo se pueden implementar también en pequeñas corrientes naturales de agua. Fig 1 y 2
El aforo volumétrico consiste en medir el tiempo que gasta el agua en llenar un recipiente de volumen conocido para lo
cual, el caudal es fácilmente calculable con la siguiente ecuación:Q=V/t.
AFORO CON VERTEDEROS Y CANALETAS. Se utilizan principalmente en la medición de caudales en pequeñas
corrientes, en canales artificiales y de laboratorio; su uso en corrientes naturales es muy restringido. Un funcionamiento
típico de un vertedero para aforar corrientes naturales se muestra en la Fig 3.
AFORO CON TUBO DE PITOT. Su mayor aplicación se encuentra en la medición de velocidades en flujo a presión, es
decir, flujos en tuberías. Sin embargo, también se utiliza en la medición de velocidades en canales de laboratorio y en
pequeñas corrientes naturales. Es tubo de pitot permite medir la velocidad de la corriente a diferentes profundidades, por lo
cual se puede conocer la velocidad media en la sección, que multiplicada por el área de ésta, produce el caudal de la
corriente.
AFORO CON TRAZADORES FLUORESCENTES 0 COLORANTES. El empleo de colorantes para medir la velocidad
del flujo en corrientes de agua es uno de los métodos más sencillos y de mayor éxito. Una vez elegida la sección de aforo,
en la que el flujo es prácticamente constante y uniforme se agrega el colorante en el extremo de aguas arriba y se mide el
tiempo de llegada al extremo de aguas abajo. Conocida la distancia entre los dos extremos de control, se puede dividir esta
por el tiempo de viaje del colorante, obteniéndose así la velocidad superficial o subsuperficial de la corriente liquida. La
velocidad media de flujo se obtendrá dividiendo la distancia entre los dos extremos o puntos de control, por el tiempo
medio de viaje.
Si se inyecto un colorante de tipo brillante, como la eosina, y si se suspende horizontalmente una lamina brillante, de
longitud conocida, en un sitio aguas debajo de la inyección, es posible detectar los instantes en que desaparecen y aparece
el colorante en los extremos de dicha lamina. La medida del tiempo que transcurre entre los instantes de desaparición y
aparición del colorante se puede emplear como representativo del tiempo medio del flujo a lo largo de la lamina. La
velocidad media superficial del flujo se obtendrá dividiendo la longitud de la lamina por el tiempo medio del flujo.
Otros colorantes, común y eficazmente empleados como trazadores, son la fluoresceína, el rojo congo, el permanganato de
potasio, la rodamina b y el pontacil rosa B brillante. Este último es especialmente útil en estudios de dispersión de
contaminantes en el agua. En los últimos años se han logrado considerables mejoras en las técnicas de medición con
trazadores fluorescentes, especialmente con la rodamina B, rodamina WT, las sulforrodaminas B y G la uramina y el
bromuro 82.
AFOROS CON TRAZADORES QUÍMICOS Y RADIOACTIVOS. Es un método muy adecuado para corrientes
turbulentas como las de montañas. Estos trazadores se utilizan de dos maneras: como aforadores químicos, esto es, para
determinar el caudal total de una corriente y como medidores de velocidad de flujo.
En los aforos químicos y radioactivos, se inyecta una tasa constante qt, de la sustancia química, radioactiva o trazador, de
concentración conocida, Cti, a la corriente cuyo caudal, Q, desee determinarse y cuya concentración de la sustancia, Ca , en
la corriente, también se conoce. A una distancia corriente abajo, suficientemente grande para asegurar que se han mezclado
totalmente el trazador y el agua, se toman muestras de ésta, y se determina la concentración de la sustancia química o
radioactiva, Ct. ( Fig 4 )
El caudal de la corriente se puede determinar, entonces, empleando la siguiente ecuación.

6. En su empleo como medidores de velocidad, los trazadores químicos y radioactivos se inyecta aguas arriba del primer
punto de control de la corriente. Se calcula el tiempo de paso del prisma de agua que contiene el trazador entre dicho punto
de control y otro situado aguas abajo a una distancia previamente determinada. El cociente entre esta distancia y el tiempo
de paso es la velocidad media de la corriente.
Cuando se emplea la sal común ( NaCl ) como trazador químico, se mide el tiempo de paso entre los dos puntos de control,
utilizando electrodos conectados a un amperímetro, esto es, un conductivímetro. Este método de medición es posible
debido a que la sal inyectada aumenta la concentración de sólidos disueltos y, por lo tanto, la conductividad del agua.
AFORO CON FLOTADORES. Son los más sencillos de realizar, pero también son los más imprecisos; por lo tanto, su
uso queda limitado a situaciones donde no se requiera mayor precisión. Con este método se pretende conocer la velocidad
media de la sección para ser multiplicada por el área, y conocer el caudal, según la ecuación de continuidad.
Q = velocidad *área
Para la ejecución del aforo se procede de la siguiente forma. Se toma un techo de la corriente de longitud L; se mide el área
A, de la sección, y se lanza un cuerpo que flote, aguas arriba de primer punto de control, y al paso del cuerpo por dicho
punto se inicia la toma del tiempo que dura el viaje hasta el punto de control corriente abajo. Como se muestra en la
siguiente figura.
La velocidad superficial de la corriente, Vs, se toma igual a la velocidad del cuerpo flotante y se calcula mediante la
relación entre el espacio recorrido L, y el tiempo de viaje t.
Se considera que la velocidad media de la corriente, Vm, es del orden de 0.75Vs a 0.90 Vs, donde el valor mayor se aplica a
las corrientes de aguas más profundas y rápidas ( con velocidades mayores de 2 m/s. Habitualmente, se usa la siguiente
ecuación para estimar la velocidad media de la corriente. Vm = 0.85VS.
Si se divide el área de la sección transversal del flujo en varías secciones, de área Ai, para las cuales se miden velocidades
superficiales, Vsi, y se calculan velocidades medias, Vmi, el caudal total se podrá determinar como la sumatoria de los
caudales parciales qi, de la siguiente manera:
Se pueden obtener resultados algo más precisos por medio de flotadores lastrados , de sumersión ajustable, como muestra
en la figura 5. Estos flotadores consisten en un tubo delgado de aluminio, de longitud Lfl, cerrado en ambos extremos y con
un lastre en su extremo inferior, para que pueda flotar en una posición próxima a la vertical, de tal manera que se sumerjan
hasta una profundidad aproximadamente de 25 a 30 cm sobre el fondo, y emerjan unos 5 a 10 cm.
La velocidad observada de flotador sumergido, Vf, permite la determinación de la velocidad media de la corriente, Vm, a lo
largo de su curso, por la siguiente formula experimental:
donde y es la profundidad de la corriente de agua.

7. AFORO CON MOLINETE O CORRENTÓMETRO. El principio de la medición de velocidad con molinete es el
siguiente: Supóngase un molinete puesto en un punto de una corriente que tiene una velocidad V. La longitud S, es el
recorrido de una partícula fluida moviéndose a lo largo del contorno completo de la línea que determina una vuelta de la
hélice. La situación es análoga al suponer quieta el agua y el molinete desplazándose
a través de ésta con velocidad V. Para un desplazamiento S, la hélice también dará una vuelta.
Para un movimiento uniforme,
El espacio, S, recorrido por la hélice, o por la partícula líquida a través de ésta, se representa por el número de rotaciones,
N, que da el molinete en t segundos.
Luego
Como existen fricciones en las partes mecánicas del aparato, es necesario introducir un coeficiente de corrección, b.
Entonces
Y haciendo , la frecuencia de giro, se tiene: V=b*n
Con la sensibilidad del aparato se hace sentir a partir de determinada velocidad mínima, a, que en general, es del orden de
1 cm/s, por debajo de la cual el aparato no se mueve, la ecuación del aparato se transforma en:
V= a+ b*n
Ecuación que corresponde a una línea recta. Los aparatos vienen con su respectiva ecuación de calibración, dependiendo
del tipo de molinete y de la casa productora, o tabuladas las velocidades en función del número de revoluciones por
minuto.

8. CARGA
h μ k C Q
0.118 0.6 1 0.81834956 9.36093E-06
0.161 0.6 1 0.81834956 4.42627E-05
0.19 0.6 1 0.81834956 0.000101316
0.248 0.6 1 0.81834956 0.000383855
Gasto del Tirantes en
Evento
vertedor
(m3
/s) el río (m)
1 9.36093E-06 0.1895
2 4.42627E-05 0.2204
3 0.000101316 0.2428
4 0.000383855 0.285
MEMORIA DE CÁLCULO
1. Calcular el gasto Q, en m3
/s, en el
vertedor triangular, para cada una de las
cargar registradas en la Tabla 2.
Q = C h5/2
Donde:
h: carga sobre el vertedor, en m
C: coeficiente de descarga del
vertedor
C = (8/15)
3. Obtener la ecuación de ajuste de
n
g: aceleración de la gravedad la forma Q = ky para los datos
θ: ángulo en el vértice del vertedor
de aforo, 60°
μ: coeficiente experimental que
depende de h y θ, según la figura 7.9
de la referencia 1
K: coeficiente que depende de B/h,
según la figura 7.1 de la referencia 1
B: ancho del canal de aproximación
B= 1.065m
de la Tabla 5, empleando una
regresión lineal simple.
4. Dibujar en un plano Q-y los
puntos experimentales de la
Tabla 5 y la curva de ajuste del
punto 3
2. Presentar en una tabla los
valores de gasto que
corresponde a cada tirante
medido en el cauce, Tabla 5.
0.0004
0.0003
0.0002
0.0001
0
0.18 0.23 0.28
Puntos
experiment
ales
Potencial
(Puntos
experiment
ales)

9. 5. Obtener la velocidad superficial
como
Donde:
Vs i : velocidad superficial del
evento i, en m/s
vs i = d/ti
d (m) t (s) vs i (m/s)
3 13.7 0.2189781
3 15.99 0.18761726
3 15 0.2
Σ = 0.60659536
vsup = 0.20219845
6. Calcular la velocidad media V, en
m/s, a partir del promedio de las
velocidades puntuales de la tabla
3 y la superficial del punto 5
c) Indicar los puntos de
medición de las velocidades
con su valor
correspondiente, según la
tabla 3.
Utilizando el software “Autocad”, tenemos:
8. Determinar el área hidráulica A,
en m, de la sección de aforo.
Utilizando el software “Autocad”,
se tiene un área de:
A = 0.1555 m2
V = 0.16063969 m/s
9. Dibujar la curva de velocidades
de la sección de aforo
0.14 0.15 0.16 0.17
7. Dibujar a escala en un plano:
a) La sección transversal de
aforo, en color negro a partir
de los datos de la Tabla 1
b) La superficie libre del agua
en color azul
0
0.05
0.1
0.15
0.2
0.25

10. 10. Determinar el gasto QSV, en m3
/s, como: QSV = V A
Donde:
QSV: gasto por sección velocidad, en m3
/s
QSV = (0.16063969 m/s)( 0.1555 m2
) QSV =0.024979471 m3
/s
11. Calcular el error relativo en por ciento, entre los gastos Q4 y QSV
e = 64.97%
CUESTIONARIO
1. . ¿Para qué se emplea un molinete y en qué técnica de aforo se usa?
Se emplea para medir velocidades y es usada en el método de sección-velocidad
2. ¿Qué características físicas debe tener la sección transversal del cauce para que ésta sea una sección de control?
Debe tener la relación única de tirante contra gasto