Fisica C, ESPOL

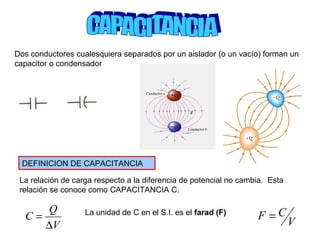
1. Dos conductores cualesquiera separados por un aislador (o un vacío) forman un
capacitor o condensador
DEFINICION DE CAPACITANCIA
La relación de carga respecto a la diferencia de potencial no cambia. Esta
relación se conoce como CAPACITANCIA C.
C Q
= La unidad de C en el S.I. es el farad (F)
V
D
V
F = C

2. CAPACITOR DE PLACAS
PARALELAS
ò E · dA = qencerrada
0 e
0
 
DV = E d Þ E = DV 0 0
d
E0 dA
E A = Q
0 e
0
A Q
d
0 e
DV =
Q = e
A
0 D d
d
V
C 0A = e

3. PROBLEMA
Calcule el área que debe tener la placa de un capacitor de placas paralelas
para que su capacitancia sea de 1.0 F. Suponga que la separación entre sus
placas es de 1.0 cm.
e A Cd
d
0
0
e
C = A Þ =
( )
A 1.0 F 0.01
m ´ -
=
8.85 10 12 C 2 / Nm
2
A =1129943503m2
Si la placa fuera cuadrada, cada
lado mediría:
l = 336147m

4. CAPACITOR CILINDRICO
b
V V E ds
a
b a
 
- = -ò ×
EA = Q Þ E = l
l
e rl
0 0 2p e
E = 2kl
r
DV = 2kl ln b = 2 k Q
ln
V Edr 2kl dr a
D = -ò = - òb
b
a a
r
b
l
a
C
Q =
k b
ö a
çè
l
V
÷ø
æ
=
D 2 ln

5. CAPACITOR ESFERICO
- = -òb
b a a V V Edr
E = k Q
Donde: r2
V kQ r dr b
a ò D = -2
V kQ 1 1 1
ö çè
÷ø
ö çè
æ - = ÷ø
D = - æ-
b a
kQ
r
Q ab
=
V kQ b a ( ) C
ö çèæ - = D
÷ø
ab
k b a
V
-
=
D
Demuestre que si el radio
exterior de la esfera se acerca
al infinito, entonces:
C a 0 = 4pe

6. COMBINACION DE CAPACITORES
En paralelo
q CV 1 1 =
q C V 2 2 =
q q (C C )V 1 2 1 2 + = +
Q = +
1 2 C C
V
1 2 C C C equiv = +
En una conexión en paralelo el potencial es el mismo.

7. En serie
V = q
1 C
1
V = q
2
2 C
ö
÷ ÷ø
æ
ç çè
+ = +
1 2
1 2
1 1
C C
V V q
1 1 1
q = +
C C
1 2
V
1 = 1 +
1
C C C equiv
1 2
Para una combinación en serie, la carga en los capacitores es la misma.

8. ENERGIA ALMACENADA EN UN CAPACITOR
Usted tiene tres capacitores y una batería. ¿Cómo combinaría los capacitores
y la batería en un circuito de modo que los capacitores almacenaran la máxima
energía posible?

9. DENSIDAD DE ENERGÍA
u = Energía ( )
Volumen
Ed
Ad
A
= = æ e
ö d
çèu CV
Ad
2
0
2
1
2
1
2
÷ø
2
u = 1e E
0 2

10. Calcule la capacitancia equivalente entre los puntos a y b y complete la tabla
mostrada. Vab = 24V
(C)
μF
Q (mC) V(V) U(J)
C1 12
C2 12
C3 10
C4 15
C5 4
e
a · b d ·
1 = 1 + Þ ¢ =
¢
C F C6 2
C
6m
1
15
10
1 = 1 + Þ =
C F
1
C eq
eq
8m
24
12
Q C V F Q C eq ab 8m 24 192m 1 1 = = ´ Þ =
V Q ad 16
m V
V = 8
V db C
= 1 = =
F
C
192
12
1
m
192
96
48
48
16
8
4.8
3.2
8
8
32
16
Q C V F V C db 12m 8 96m 2 2 = = ´ =
Q V C V F C db 8 6m 48m 34 34 = = ´ =
C1
C2
C3 C4
C5
C6
V Q de 4.8 eb 3.2
V V V
F
m
= 3 = = Þ =
C
C
48
10
3
m
Q C V F V C db 4m 8 32m 5 5 = = ´ =
Q C V F V C db 2m 8 16m 6 6 = = ´ =

11. CAPACITORES CON DIELECTRICOS
Cuando se inserta el dieléctrico, los experimentos muestran que la diferencia de
potencial disminuye a un valor más pequeño V.
Cuando se retira el dieléctrico, la diferencia de potencial recupera su valor original
V0 , lo que demuestra que las cargas originales de las placas no han cambiado.
C = Q
C = Q (sin dieléctrico)
(con dieléctrico)
0 V
0
V

12. C = Q
C = Q (con dieléctrico)
(sin dieléctrico)
0 V
0
V
Cuando el espacio entre las placas está ocupado totalmente por el dieléctrico,
la proporción de C a C0 recibe el nombre de constante dieléctrica del
material k.
÷ ÷ø ö
æ
k C ( ) 0 Cuando Q es constante
ç çè
=
definicion de constante
dieléctrica
0 C
k = V
V

13. CARGA INDUCIDA Y POLARIZACION
Moléculas polares sin
campo eléctrico aplicado
Moléculas polares, con
campo eléctrico aplicado
Moléculas no polares sin
campo eléctrico aplicado
Moléculas no polares con
campo eléctrico aplicado

14. La polarización de un dieléctrico en un campo eléctrico E da origen a capas finas de
cargas ligadas en las superficies, y esto crea densidades de cargas superficiales σi y
-σi

15. PROBLEMA
Un capacitor se construye a partir de dos placas cuadradas de lados l y
separación d . Un material de constante dieléctrica k se inserta una distancia
x dentro del capacitor como se muestra en la figura.
a) Encuentre la capacitancia equivalente del dispositivo.
b) Calcule la energía almacenada en el capacitor si la diferencia de potencial
es ΔV.
c) Encuentre la magnitud y la dirección de la fuerza ejercida sobre el
dieléctrico, suponiendo una diferencia de potencial constante ΔV. Ignore la
fricción
x
ℓ
k d
( )
d
l x l
a C C C k xl eq
1 2 ) e e
= + = 0 + 0 -
d
Ceq = 0 + 2 - e
(kxl l xl)
d
= 0 [l2 + xl(k -1)]
d
Ceq
e

16. x
ℓ
k d = 0 [l2 + xl(k -1)]
d
Ceq
e
0 [ 2 ( 1)]( )2
b U = CV = e + - D
) 1 2 l xl k V
2 2
d
 c ) F = - dU ˆ = - e 0 - 1 D 2
ˆ
[l(k )]( V ) i
d
i
dx
2
Dirigida hacia la izquierda ( ) l(k )i
d
F V 1 ˆ
2
2
= -e 0 D - 

17. Carga libre
Carga inducida
--------
++++++++ A
q(carga libre)
E dA q E A q E q
0
ò  
= Þ = ÞÞ = 0
0
0
0
0.
e e e
k dieléctrico E 
- ¢ Þ =
q q
A
- ¢ =
E A q q E k
k
0
0
0 e e
q¢(carga inducida)
0 E 
superficie
Gaussiana

18. - ¢ Þ =
q q
A
- ¢ A =
E A q q E k
k
0
0
0 e e
E dA q E A q E q
0
ò  
= Þ = ÞÞ = 0
0
0
0
0.
e e e
q ¢ = q æ 1 -
1
÷ø
- ¢ q
k q ¢ = kq - q A
kq kq
A
=
0 0 e e
ö k
çè
ò ¢ E dA =
q - q k
0
.
e
 
ò
1 1
ö çè
÷ø
- æ -
=
0
 
.
e
k
q q
E dA k

19. Un capacitor de placas paralelas es cargado con una batería hasta una carga
Q0, como se muestra en la figura. Luego, la batería es removida, y una loza de
material que tiene una constante dieléctrica K se inserta entre las placas.
Calcule la energía guardada en el capacitor antes y después que el dieléctrico
se ha insertado.
La energía guardada sin dieléctrico es:
Cuando se desconecta de la batería y se inserta el
dieléctrico, la carga en el capacitor no cambia. Por lo
tanto, la energía guardada en presencia del dieléctrico es:
Pero la capacitancia en presencia del dieléctrico es:
C=kC0 , así que U es:

20. El campo eléctrico no uniforme cerca de los filos del capacitor de placas
paralelas causa que el dieléctrico sea halado hacia el capacitor. Note que el
campo actúa sobre las cargas inducidas de la superficie, las cuales están
distribuidas no uniformemente.

21. Se observa las cargas inducidas en el dieléctrico entre las placas del
capacitor cargado. Note que la densidad de carga inducida en el
dieléctrico es menor que la densidad de carga en las placas.

22. Un capacitor de placas paralelas tiene un área A y separación entre las
placas d. Una loza metálica descargada de espesor a se inserta en la mitad
entre las placas.
a) Calcule la capacitancia del dispositivo.
1 = 1 +
1
C C C
1 2
A
= e e
C A
( ) ( )
2
1
2
1 1
0 0
d a
d a
-
+
-
Observe que C se aproxima al infinito cuando a se acerca a d. ¿Por qué?

23. b) Muestre que la capacitancia del dispositivo no es afectada cuando el
espesor de la loza se hace infinitésimamente pequeño.
La cual es la capacitancia original
c) Demuestre que la respuesta de la parte (a) no depende del lugar donde la
loza se inserta.
Imaginemos que la loza es movida hacia arriba de modo que la distancia
entre el filo superior de la loza y la placa superior sea b. Luego, la distancia
entre el filo inferior de la loza y la placa de abajo sería: d - b – a. Como en la
parte (a), hallamos la capacitancia total de la combinación en serie.
Este es el mismo resultado
que en (a). Es
independiente del valor de
b.

24. En el ejemplo anterior encontramos que se puede insertar una loza metálica
entre las placas de un capacitor y considerar la combinación como dos
capacitores en serie. La capacitancia resultante fue independiente de la
ubicación de la loza. Además, si el espesor de la loza se aproxima a cero, la
capacitancia del sistema se aproxima a la capacitancia cuando la loza está
ausente.

25. Un capacitor de placas paralelas se construye usando tres materiales
dieléctricos. Se puede suponer que l >> d. Encuentre una expresión para la
capacitancia del dispositivo en términos del área de placa A y d, k1 , k2. y k3

26. Considere el circuito mostrado en la figura, donde C1 = 6.00μF, C2 = 3.00μF, y
ΔV = 20.0V. El capacitor 1 es cargado primeramente al cerrar el switch S1.
Luego el switch S1 se abre y el capacitor cargado se conecta al capacitor
descargado al cerrar el switch S2. Calcule la carga inicial de C1 y la carga final
de cada uno.

27. Para el sistema de capacitores mostrado en la figura, calcule:
a)La capacitancia equivalente del sistema.
b)La carga en cada capacitor.
c)La diferencia de potencial a través de cada capacitor.

28. Calcule la capacitancia equivalente entre los puntos a y b en la combinación
de capacitores mostrados en la figura

29. Considere dos alambres largos, paralelos y con cargas opuestas de radio d
con sus centros separados por una distancia D. Suponiendo que la carga está
distribuida uniformemente sobre la superficie de cada alambre, demuestre que
la capacitancia por unidad de longitud de este par de alambres es:
El campo eléctrico debido a la carga sobre el alambre positivo es
perpendicular al alambre, radial y de magnitud:
La diferencia de potencial entre los alambres debido a la presencia de esta
carga es:

30. La capacitancia por unidad de longitud es:

31. Un capacitor de placas paralelas tiene una carga Q y placas de área A. ¿Cuál
es la fuerza que actúa sobre una placa para atraer sobre ella a la otra placa?

32. (b) Calcule la constante de fuerza del
resorte
La fuerza que estira un resorte es:

33. Cada resorte se estira por una distancia
igual a:

34. Un capacitor tiene placas cuadradas, cada una de lado a, formando un ángulo
Ө entre si. Demuestre que, para Ө pequeño, la capacitancia está dada por:
ö çè
÷ø
C a
= æ -
d
a
d
2
1
2
0 e q
e
d xsen
q
dC = adx
0
+
- =e ò + q
C a (d xsen ) dx 1
0
x
= e æ + q De acuerdo
ö çè
sen dx
d
C a
d
1
0 1
-
ò ÷ø
al binomio de
Newton
÷ø
C = e a ò æ1- x
0 q
sen dx
d
d
ö çè
C a a ò ÷ø
dx
x
e 0 1 q
d
= æ -
d
ö çè
0
ö
÷ ÷ø
æ
ç çè
a a
C a
= -
d
d
2
2
C a
= æ -
a
ö çè
÷ø
e q 0 1
d
2
d
2
0 e q
x
dx
q
a
d
dA = adx

35. PROBLEMA
+ + + + + + + + + + + + + + + + + + + + +
- - - - - - - - - - - - - - - - -
+ + + + + + + + + + + + + + + + +
- - - - - - - - - - - - - - - - - - - - - - - - - - -
-

36. - - - - - - - - - - - - - - - - -
+ + + + + + + + + + + + + + + + +
- - - - - - - - - - - - - - - - - - - - - - - - - - -
-
(c) Calcular la intensidad del campo eléctrico en la parte sin dieléctrico.

37. (d) Calcular la intensidad del campo eléctrico en el dieléctrico.
(e) Calcular la diferencia de potencial entre las placas.
Se tomará una superficie recta perpendicular a las placas desde abajo
hacia arriba.
(f) Calcule la Capacitancia al estar colocado el dieléctrico.