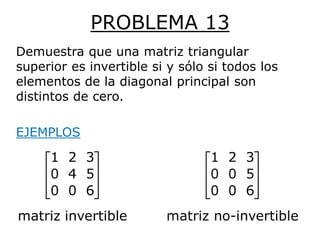
1. PROBLEMA 13
Demuestra que una matriz triangular
superior es invertible si y sólo si todos los
elementos de la diagonal principal son
distintos de cero.
EJEMPLOS

2. PROBLEMA 13
• El problema es del tipo “si y sólo si”, lo que
significa que se tienen que hacer dos
demostraciones: una de ida, y una de
regreso.
• La demostración de ida es:
– suponer que la matriz triangular superior es
invertible, y demostrar que todos los
elementos de su diagonal no son cero.
• La demostración de regreso es:
– suponer que los elementos de la diagonal son
distintos de cero, y demostrar que la matriz es
invertible.

3. PROBLEMA 13
LA IDA
• Supongamos que la matriz triangular
superior A es invertible. Debemos
probar que en la diagonal no hay
ceros.
• Sabemos dos cosas:
– A es triangular superior (hay puros
ceros debajo de la diagonal).
– A es invertible.

4. PROBLEMA 13
LA IDA
• Como A es invertible, entonces:
– Teorema 12 (Hoffman):
A es equivalente por filas a la matriz
identidad de la misma dimensión.
• La idea es:
– supongamos que algún elemento de la
diagonal es cero. ¿Cuál es la
contradicción?

5. PROBLEMA 13
LA IDA
ILUSTRACION
Tomemos una matriz triangular
superior y hagamos cero algún
elemento de su diagonal
principal.
Según el teorema, deberíamos
de poder escrbir el segundo
renglón de la matriz identidad
como combinación lineal de las
filas
Pero… ¿lo podemos lograr?

6. PROBLEMA 13
LA IDA
ILUSTRACION
¿Cómo le hacemos para que se haga 1?
Si sumamos la mitad de la fila de arriba,
lo podríamos lograr. Sin embargo, el
cero que estaba a la izquierda ya sería
otro número.
Ese un problema. ¿Podemos lograr un 1
con otras filas? No, porque por
definición todo lo de abajo es cero.
¿Qué significa esto? No se puede lograr
llevar esta matriz a la matriz identidad.

7. PROBLEMA 13
LA IDA
IDEA
Podemos suponer que el renglón i-ésimo de A
empieza con cero (es decir, estamos suponiendo
que A si tiene un cero en su diagonal):
Luego, podemos intentar probar que el renglón
i-ésimo de la matriz indentidad no podrá escribirse
como CL de los demás renglones de A:

8. PROBLEMA 13
EL REGRESO
• Ahora, supongamos que la matriz
triangular superior A no tiene ceros
en la diagonal. Debemos probar que
es invertible.
• Usamos el mismo teorema de hace
rato. Parece que el regreso es más
fácil que la ida.

9. PROBLEMA 13
EL REGRESO
IDEA
• Lo que debemos hacer es probar que A es
equivalente por filas a la matriz identidad.
• Pero eso es sencillo:
– cada fila la dividimos entre su primer elemento no
nulo (que estará sobre la diagonal principal, por
hipótesis).
• Así, toda la diagonal se hace de puros 1’s, y
de ahí se ve que cada renglón de la matriz
identidad se puede escribir como CL de
renglones de A (parecido a una eliminación
gaussiana).

10. PROBLEMA 13
EL REGRESO
ILUSTRACION
Le sumamos el
renglón 2 y le Le sumamos el Obtenemos la
restamos el renglón 3. identidad.
renglón 3.

11. • ¿Cómo le hacemos para el problema
14?
• En resumen: jugar con la
multiplicación de matrices.
• Próximamente…