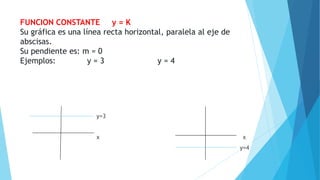
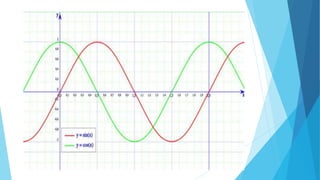
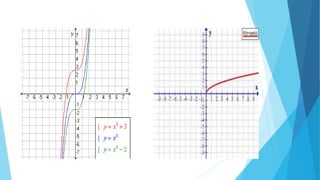
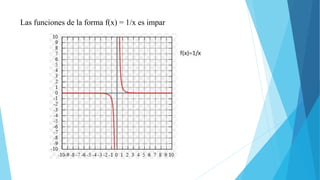
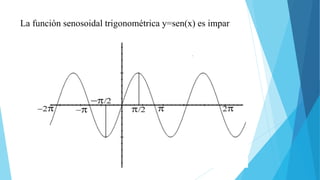
Este documento explica las características de las funciones constantes, pares e impares. Las funciones constantes tienen pendiente cero y su gráfica es una línea horizontal. Las funciones pares son simétricas respecto al eje y y satisfacen la ecuación f(-x)=f(x), mientras que las funciones impares satisfacen f(-x)=-f(x) y son simétricas respecto al origen luego de una rotación de 180 grados. Algunos ejemplos de funciones pares son x^2, cos(x) y valor absoluto, m

1. UNIVERSIDAD NACIONAL DE CHIMBRAZO
SISTEMA NACIONAL DE NIVELACIÓN Y ADMISIÓN
ASIGNATURA DE MATEMATICAS
INTEGRANES: ISRAEL PAUCAR
DIANA PILATAXI
LIGIA PILAMUNGA
Paralelo: EM2
FECHA: 2015-07-20

2. FUNCION CONSTANTE y = K
Su gráfica es una línea recta horizontal, paralela al eje de
abscisas.
Su pendiente es: m = 0
Ejemplos: y = 3 y = 4
y=3
x x
y=4

3. La ecuación del eje de abscisas (OX) es: y =0
La ecuación de una recta vertical, paralela al eje de ordenadas, es: x = K. Hay
que hacer notar que estas rectas no representan funciones, porque las
coordenadas de sus puntos tienen todas el mismo valor de la abscisa, luego un
único valor de x tiene infinitos valores de y diferentes, por lo tanto no son
funciones.
 Y x=5 x=2 y
x x

4. FUNCION PAR
Una función par es cualquier función que satisface la relación f(x)=f(-x)
y si x es del dominio de f entonces -x también.
Desde un punto de vista geométrico, una función par es simétrica con
respecto al eje y, lo que quiere decir que su gráfica no se altera luego de
una reflexión sobre el eje y.
Ejemplos de funciones pares son el valor absoluto, x 2 , x 4 , cos(x), y
cosh(x).
La mejor manera de ver esto es gráficamente:

5. La función cuadrática al girar alrededor del eje y tiene la
misma grafica la función, es decir la función es par.
Toda función cuadrática de la forma y=ax² si está situada
en el eje y es par, si la función se desplaza hacia la derecha
o hacia la izquierda deja de ser par y se convierte en
función impar.
La función coseno también es par, y si se desplaza hacia la
derecha o hacia la izquierda siempre que el desfase sea de
180 grados o pi radianes. Esto se debe a que la función
coseno es periódica, si se cambia la frecuencia de la
función coseno también deberá variar la distancia a la que
su desfase le permitirá tener siempre la misma grafica
alrededor del eje y ejemplo para cos(2x) el desfase para
que sea par será 90 grados o pi/2

7. La función valor absoluto en el origen es par, y
toda función valor absoluto que este dentro de este
eje será par por ejemplo y= ‫׀‬x‫2+׀‬ , y = ‫׀‬x‫3-׀‬

8. Definición formal
El término función par suele referirse a una clase especial de funciones de variable
real: una función f: R → R es una función par si para −X ∈ R se cumple la
siguiente relación:
f(x)= f(-x)
La definición anterior puede generalizarse a funciones sobre dominios más
generales. Si A es un conjunto con cierta estructura algebraica en la que existan
inversos aditivos (por ejemplo, los números complejos C), una función par sería
toda función:
𝑓: 𝐴 → 𝐵
𝑎 → 𝑏 = 𝑓(𝑎)
Que cumpla:
∀𝑎 ∈ 𝐴: 𝑓 −𝑎 = 𝑓(𝑎)
La definición de función par presupone que si 𝑎 ∈ 𝐴entonces
necesariamente −𝑎 ∈ 𝐴, de no ser así no se podría definir 𝑓 −𝑎 .

9. Ejemplo
La función:
f(x)= 𝑥2 + 1
Es par ya que para cualquier valor de x se cumple:
𝑓 𝑥 = (−𝑥)2 + 1
𝑓 𝑥 = (−1. 𝑥)2 + 1
𝑓 𝑥 = (−1)2. 𝑥2 + 1
𝑓 𝑥 = 1. 𝑥2
+ 1
𝑓 𝑥 = 𝑥2
+ 1
𝑓 𝑥 = 𝑓(𝑥)
Demostrando que la función es par.
Si x=2, entonces:
𝑓 −2 = (−2)2 + 1 = 4 + 1 = 5 = 22 + 1 = 𝑓(2)

10. Función impar
Una función impar es cualquier función que
satisface la relación:
f(-x)= f(-x)
Para todo x en el dominio de f.
Desde un punto de vista geométrico, una función
impar posee una simetría rotacional con respecto al
origen de coordenadas, lo que quiere decir que su
gráfica no se altera luego de una rotación de 180
grados alrededor del origen.

11. Podemos ver que:
𝑓 −𝑥 = (−𝑥)3
𝑓 𝑥 = (−1. 𝑥)3
𝑓 𝑥 = (−1)3. 𝑥3
𝑓 𝑥 = −1. 𝑥3
𝑓 𝑥 = −1. 𝑓(𝑥)
𝑓 𝑥 = −𝑓(𝑋)
Y esta función si pasa por el punto (0,0).
Por ejemplo las funciones lineales son funciones impares.
Ya que al girar la recta para el otro lado no es igual

14. Las funciones de la forma f(x) = 1/x es impar

15. La función senosoidal trigonométrica y=sen(x) es impar

16. Gracias por su atención
cualquier inquietud pregunten ala lisen
porque la lisen sabe mas que nosotros