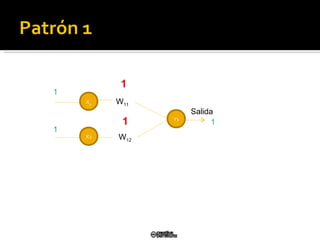
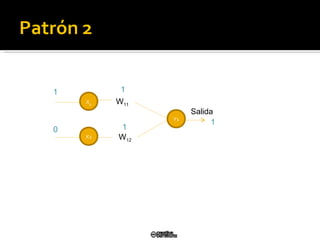
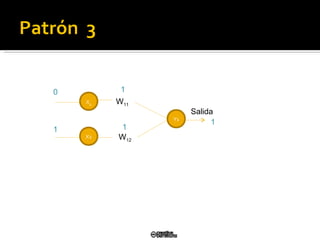
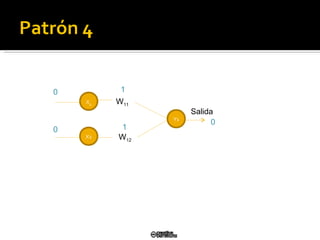
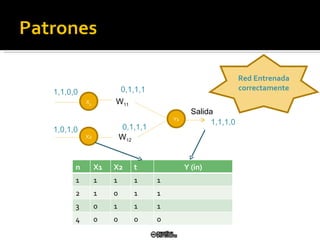
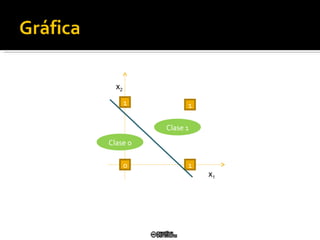
El documento describe el modelo de perceptrón simple desarrollado por Frank Rosenblatt en 1958. El perceptrón puede clasificar patrones de entrada de manera binaria (0/1) dependiendo de los pesos sinápticos. El algoritmo de aprendizaje actualiza los pesos para minimizar el error entre la salida del perceptrón y la salida deseada, convergiendo en un tiempo finito si los patrones son linealmente separables.

1. Roberth Gustavo Figueroa Díaz -- Camilo Javier Solís Álvarez rgfigueroa@utpl.edu.ec -- [email_address] Universidad Técnica Particular de Loja Escuela de Ciencias de la Computación LOJA - ECUADOR

2. En 1958 el psicólogo Frank Rosenblatt desarrolló un modelo simple de neurona basado en el modelo de McCulloch y Pitts y en una regla de aprendizaje basada en la corrección del error. Neuronas de entrada son discretas Función de activación de las neuronas de la capa de salida es de tipo escalón Dispositivo entrenable: determinar automáticamente los pesos sinápticos que clasifican un conjunto de patrones etiquetados

3. Modelo simple Clásico basado en el mo delo de McCulloch-Pitts Arquitectura (izquierda) y función de transferencia (derecha) de un perceptrón simple

4. El perceptrón simple tan sólo puede discriminar entre dos clases linealmente separables Ejemplo: x1 y x2 dos neuronas de entrada, la operación efectuada por el perceptrón simple consiste en:

5. Región de decisión correspondiente a un perceptrón simple con dos neuronas de entrada

6. Algoritmo de Aprendizaje (Rosenblatt, 1962) Pertenece al grupo de algoritmos fundamentados en la corrección de errores X r conjunto de patrones de entrada, r = 1,… ,N t r conjunto de clases verdaderas de dichos patrones, r = 1,….,N Variables de entrada como las de salida toman dos posibles valores: -1 y +1

7. Actualización de pesos: Si ante la presentación del r-ésimo patrón la respuesta que proporciona el perceptrón simple es correcta, no actualizaremos los pesos Si la respuesta es incorrecta los pesos se modificarán según la regla de Hebb Es decir: Reescrita queda así:  regla del perceptrón

8. La actualización de pesos únicamente podrá tomar los valores 2 , 0(cero) y -2 A nivel práctico llegar a un compromiso para el valor del ritmo de aprendizaje, Valor pequeño implica un aprendizaje lento Valor excesivamente grande puede conducir a oscilaciones excesivas de los pesos no aconsejables en el proceso de entrenamiento

9. Evolución de las regiones de decisión establecidas por el perceptrón simple

10. Inicialización de la sinapsis de la red (asignar pesos sinápticos a todas las neuronas de la red) w ij = 0 o valores aleatorios La razón de aprendizaje debe ser un valor de 0 a 1 Repetir mientras haya variación de los pesos sinápticos. Para cada par de entrenamiento n = 1...N wij (0) = 0 o valores aleatorios Para j = 1....m1 donde m1 es el número de neuronas de salida Si la señal de salida es diferente a la salida esperada, existe un error y se debe adaptar la sinapsis. Según regla:

11. Luego de adaptar la sinapsis se procede a modificar los pesos, se inicia desde el paso 2. El algoritmo se detiene en el momento en el que se consigue la salida deseada .

12. El proceso de aprendizaje es iterativo Configuración sináptica inicial con pesos pequeños aleatorios Se presentan los patrones una y otra vez, con objeto de que los pesos se ajusten iterativamente según la regla del perceptrón Rosenblatt (1962) demostró que: Si la función a representar es linealmente separable, el algoritmo anterior siempre converge en un tiempo finito y con independencia de los pesos de partida Si la función a representar no es linealmente separable, el proceso de entrenamiento oscilará El algoritmo para, cuando consigue clasificar correctamente todos los ejemplos

13. N = Número total de pares de entrenamiento  4 n = Orden de pares de entrenamiento X1 , X2 = Entradas de la red t = Salida deseada Y(in) = Salida obtenida W 11 , W 12 = Pesos sinápticos n X1 X2 t Y (in) 1 1 1 1 2 1 0 1 3 0 1 1 4 0 0 0

14. X 1 X2 W 11 W 12 Y1 Salida 0 0 0 1 1 =1 n X1 X2 t Y (in) 1 1 1 1 0 2 1 0 3 0 1 4 0 0

15. X 1 X2 W 11 W 12 Y1 Salida 1 1 1 1 1

16. X 1 X2 W 11 W 12 Y1 Salida 1 1 1 1 0

17. X 1 X2 W 11 W 12 Y1 Salida 1 1 1 0 1

18. X 1 X2 W 11 W 12 Y1 Salida 1 1 0 0 0

19. X 1 X2 W 11 W 12 Y1 Salida 0,1,1,1 0,1,1,1 1,1,1,0 1,1,0,0 1,0,1,0 Red Entrenada correctamente n X1 X2 t Y (in) 1 1 1 1 1 2 1 0 1 1 3 0 1 1 1 4 0 0 0 0

20. 1 1 1 0 x 2 x 1 Clase 1 Clase 0