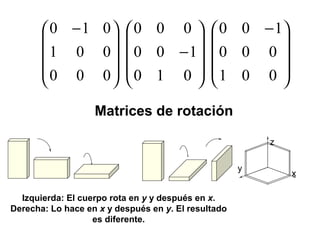
Este documento presenta información sobre varios temas matemáticos, incluidos números, operaciones, sucesiones, funciones, geometría y cálculo. Explica conceptos como números enteros, racionales, irracionales y complejos, así como la secuencia de Fibonacci. También cubre temas históricos como los matemáticos griegos y el desarrollo de conceptos como los logaritmos y los números imaginarios.