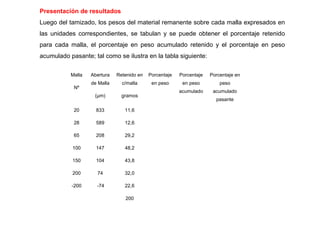
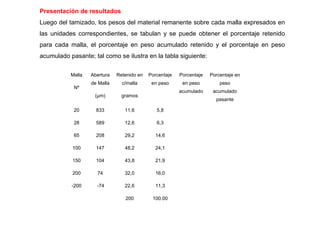
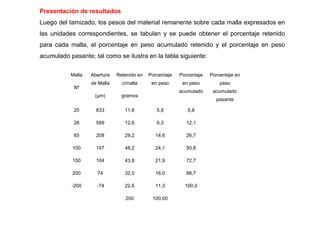
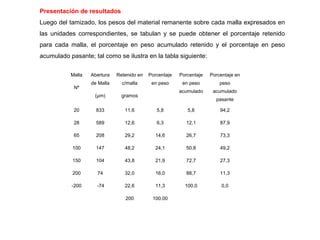
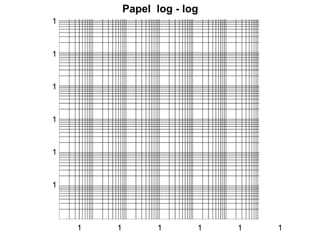
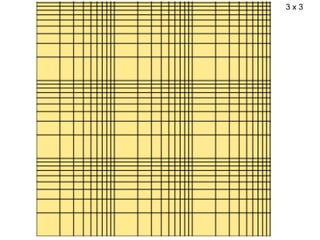
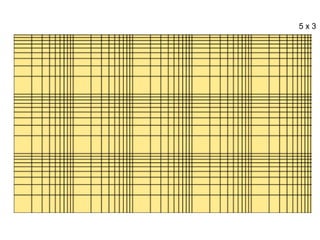
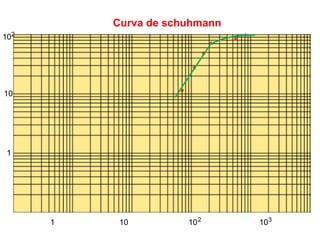
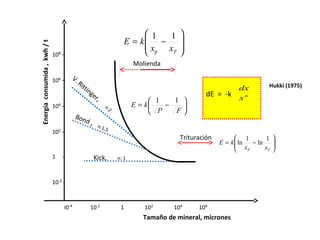
El documento trata sobre la granulometría y análisis granulométrico de minerales. Explica que existen diferentes diámetros para expresar el tamaño de una partícula mineral como el diámetro de superficie, volumen, área proyectada, etc. También describe cómo se realiza un análisis granulométrico usando tamices calibrados y cómo se presentan los resultados en una tabla con porcentajes retenidos y acumulados. Además, introduce curvas como la de Schuhmann para aproximar la distribución granulomé

1. • ¿¿ CONCENTRAR UN MINERAL ??
• MAQUILA … (COSTOS DE FUNDICIÓN Y REFINACIÓN )
US$
Extracción de mineral y comercialización
Extracción del mineral , concentración y comercialización del concentrado

2. Granulometría
Los minerales , en las primeras etapas de su tratamiento, van reduciendo sucesivamente
su tamaño
¿¿ Cuál es el tamaño de cada uno de estos fragmentos ??

3. Un fragmento de mineral, de forma irregular, no tiene una única dimensión
Para expresar su tamaño se hace en términos de una esfera equivalente
Diámetro de superficie , ds - diámetro de una esfera que tenga la misma área
superficial que la partícula mineral
Area superficial de una esfera = π d2
Diámetro ds de una esfera que tenga la
Lado : 1,4472 cm
Area superficial : 12,5663 cm2 misma área superficial que el sólido
ds = (12,5663 / π )0.5
d = 2 cm

4. Diámetro del volumen , dv - es el diámetro de una esfera del mismo volumen
que la partícula
Como en el caso anterior , el diámetro dv : 1,79553 cm
Diámetro del área proyectada , da - es el diámetro de una esfera que tenga
la misma área proyectada que el mineral cuando es visto en una dirección
perpendicular al plano de estabilidad
Diámetro del perímetro proyectado , d p - corresponde al diámetro de una
esfera que tenga el mismo perímetro proyectado que el mineral cuando es
visto en una dirección perpendicular al plano de estabilidad

5. Diámetro de arrastre, dd - es el diámetro de una esfera que tenga la misma
resistencia al movimiento que el mineral en un fluido con la misma viscosidad
y a la misma velocidad
Diámetro de caída libre , df - es el diámetro de una esfera que tenga la misma
densidad y velocidad de caída libre que el mineral en un fluído de la misma
viscosidad y densidad
Diámetro de Stokes , dSt - es el diámetro de caída libre en una región de flujo
laminar ( Reynolds = 0,2 )
dSt = ( dv3 / dd ) 1/2

6. Diámetro de la superficie del volumen específico , d vs - es el diámetro de
una esfera que tenga la misma relación de área superficial con respecto al
volumen como el mineral
dvs = dv3 / ds2
Diámetro estadístico de Martin , dM - es el equivalente estadístico del
diámetro del área proyectada da
Diámetro estadístico de Feret , dF - es el equivalente estadístico del diámetro
del perímetro proyectado dp
Diámetro de tamizado , dA - es el ancho mínimo de una abertura de malla
cuadrada a través de la cual pasa el mineral

7. Para minerales en sedimentación , es conveniente expresar su tamaño en
términos del diámetro de Stokes
Para la medición de partículas en microscopía, los microscopios proporcionan
los diámetros del volumen , de superficie, de área proyectada , perímetro
proyectado, de Feret
Para clasificación por tamaños, es muy útil el diámetro de tamizado dA

10. Los tamices son mallas calibradas de aberturas de igual tamaño.
Se designa a cada tamiz un número que corresponde al número de aberturas cuadradas en la malla por
pulgada lineal
Por ejemplo, el tamiz No 100 corresponde a 100 aberturas lineales por pulgada
La relación más usada entre el tamaño de abertura de una malla y la siguiente sigue una progresión
geométrica de razón 21/2
•Tyler Standard – USA
•AFNOR – Francia
•BESA - British Engineering Standards Association
•SIEVE Series – ASTM USA
•DIN – Alemania

11. 1 Pulgada 1 pulgada
1 2 3 4 51 2 3 4 5

12. Tabla Nº 1: Mallas de la serie Tyler, con sus respectivas aberturas
Malla Nº Abertura (µm) Malla Nº Abertura (µm) Malla Nº Abertura (µm)
75387 6 3327 100 147
2½ 63398 7 2794 115 124
3 53340 8 2362 150 104
3½ 44856 9 1981 170 88
4 37694 10 1651 200 74
5 31699 12 1397 250 61
26670 14 1168 270 53
22428 16 991 325 43
18847 20 833 400 37
15850 24 701 30
13335 28 589 26
11201 32 495 21
9423 35 417 18
7925 42 351 15
6680 48 295 13
5613 60 246 11
4699 65 208 9
3962 80 175 8
6

13. Análisis granulométrico
Es la separación de las partículas de un lote , mediante tamices, expresando
el resultado según rangos de tamaño , factibles de interpretar y utilizar
Para realizar el análisis granulométrico (tamizaje) se debe disponer los cedazos en orden
decreciente de abertura . En el fondo se ubica la bandeja
La muestra se coloca sobre el primer cedazo, y luego se tapa el conjunto llamado nido de
cedazos y se zarandea en el Rotation taper (Rotap) por el tiempo necesario. (para arena, la
norma ASTM indica 15 minutos).

14. Presentación de resultados
Luego del tamizado, los pesos del material remanente sobre cada malla expresados en
las unidades correspondientes, se tabulan y se puede obtener el porcentaje retenido
para cada malla, el porcentaje en peso acumulado retenido y el porcentaje en peso
acumulado pasante; tal como se ilustra en la tabla siguiente:
Malla Abertura Retenido en Porcentaje Porcentaje Porcentaje en
de Malla c/malla en peso en peso peso
Nº
acumulado acumulado
(µm) gramos
pasante
20 833 11,6 5,8 5,8 94,2
28 589 12,6 6,3 12,1 87,9
65 208 29,2 14,6 26,7 73,3
100 147 48,2 24,1 50,8 49,2
150 104 43,8 21,9 72,7 27,3
200 74 32,0 16,0 88,7 11,3
-200 -74 22,6 11,3 100,0 0,0
200 100.00

15. Presentación de resultados
Luego del tamizado, los pesos del material remanente sobre cada malla expresados en
las unidades correspondientes, se tabulan y se puede obtener el porcentaje retenido
para cada malla, el porcentaje en peso acumulado retenido y el porcentaje en peso
acumulado pasante; tal como se ilustra en la tabla siguiente:
Malla Abertura Retenido en Porcentaje Porcentaje Porcentaje en
de Malla c/malla en peso en peso peso
Nº
acumulado acumulado
(µm) gramos
pasante
20 833 11,6 5,8 5,8 94,2
28 589 12,6 6,3 12,1 87,9
65 208 29,2 14,6 26,7 73,3
100 147 48,2 24,1 50,8 49,2
150 104 43,8 21,9 72,7 27,3
200 74 32,0 16,0 88,7 11,3
-200 -74 22,6 11,3 100,0 0,0
200 100.00

16. Presentación de resultados
Luego del tamizado, los pesos del material remanente sobre cada malla expresados en
las unidades correspondientes, se tabulan y se puede obtener el porcentaje retenido
para cada malla, el porcentaje en peso acumulado retenido y el porcentaje en peso
acumulado pasante; tal como se ilustra en la tabla siguiente:
Malla Abertura Retenido en Porcentaje Porcentaje Porcentaje en
de Malla c/malla en peso en peso peso
Nº
acumulado acumulado
(µm) gramos
pasante
20 833 11,6 5,8 5,8 94,2
28 589 12,6 6,3 12,1 87,9
65 208 29,2 14,6 26,7 73,3
100 147 48,2 24,1 50,8 49,2
150 104 43,8 21,9 72,7 27,3
200 74 32,0 16,0 88,7 11,3
-200 -74 22,6 11,3 100,0 0,0
200 100.00

17. Presentación de resultados
Luego del tamizado, los pesos del material remanente sobre cada malla expresados en
las unidades correspondientes, se tabulan y se puede obtener el porcentaje retenido
para cada malla, el porcentaje en peso acumulado retenido y el porcentaje en peso
acumulado pasante; tal como se ilustra en la tabla siguiente:
Malla Abertura Retenido en Porcentaje Porcentaje Porcentaje en
de Malla c/malla en peso en peso peso
Nº
acumulado acumulado
(µm) gramos
pasante
20 833 11,6 5,8 5,8 94,2
28 589 12,6 6,3 12,1 87,9
65 208 29,2 14,6 26,7 73,3
100 147 48,2 24,1 50,8 49,2
150 104 43,8 21,9 72,7 27,3
200 74 32,0 16,0 88,7 11,3
-200 -74 22,6 11,3 100,0 0,0
200 100.00

18. Papel log - log
1
1
1
1
1
1
1 1 1 1 1 1

19. 3x3

20. 5x3

21. Curva de schuhmann
102
* *
*
*
*
10 *
1
1 10 10 2 103

22. La curva de distribución granulométrica se aproxima a una serie de
lineas rectas entre puntos definidos y mientras más puntos se considere
se aproxima más a la curva granulométrica original
m
 x
y = A  ..... Ecuación de Schuhmann
k
Y = % en peso pasante acumulado
X = Tamaño de abertura de malla, en micrones
K = Módulo de tamaño, en micrones, es el tamaño teórico máximo en la muestra
m = Módulo de distribución; es la pendiente de la parte recta, obtenida gráficamente

23. ¿ Preocupación por los costos
de conminución ?

24. En 1867, R.P. Von Rittinger : La energía específica consumida en la
reducción de tamaño de un sólido, es directamente proporcional a la
nueva superficie específica creada
1 1 
E = k − 
x xF 
 p 
F. Kick en 1883 , propuso que la energía requerida para producir
cambios análogos en el tamaño de cuerpos geométricamente similares ,
es proporcional al volumen de estos cuerpos
 1 1 
E = k  ln
 x − ln x 
 P F 
En 1952, Fred C. Bond, definió el parámetro k en función del work index W I
que corresponde al trabajo total necesario para reducir una tonelada corta
de material desde un tamaño teóricamente infinito hasta partículas que en
un 80 % sean inferiores a 100 micras
 1 1 
E = k − 
 P F

25. 1 1 
Energía consumida , kwh / t
E = k − 
x 
108 –  p xF 
Molienda
106 – V.
Ri
tt ing dx Hukki (1975)
er dE = -k
,  1 1  xn
104 – n:
2
E = k − 
 P F
Bon
d,
n :1 ,
2 5
10 –
Trituración  1 1 
E = k  ln
 x − ln 
 P xF 

1 - Kick, n: 1
10-2 -
I0-4 10-2 1 102 104 106
Tamaño de mineral, micrones

26. Resistencia de los minerales a la rotura
En conminución el objetivo principal ha sido derivar formas
confiables de calcular como se rompe un material particular en
una trituradora o un molino.
Es claro que algunos minerales , carbones o rocas de cantera
son mas duras que otras y el tamaño del equipo y el consumo de
energía para romper estos materiales dependerán del flujo de
alimentación , tamaño de producto deseado y dureza del material
a romper

27. ROTURA DE ROCAS
En conminución la rotura del mineral depende del
comportamiento de éste bajo la carga aplicada . La
forma de aplicación de la carga es dependiente del
equipo usado en la operación.

28. TEST DE F. BOND
Hasta mediados del siglo 20 las teorías de V. Rittinger y
Kick fueron usadas con poca frecuencia para dimensionar
equipos de trituración y molienda , debido a sus limitaciones
prácticas
A partir de 1952 se ha usado la teoría de Fred Bond como la
mejor herramienta de diseño , particularmente para la
fabricación de equipos y para evaluar y optimizar circuitos de
trituración y molienda.

29. De acuerdo a la tercera ley de la conminución de Bond, el trabajo
de entrada es proporcional a la longitud de las nuevas grietas
producidas en la rotura de la partícula e iguala el trabajo
representado por el producto, menos el representado por la
alimentación , es decir :
W = WI ( (√100 /√P ) – ( √100 /√F ))
80 80
Donde W = trabajo de entrada en kwh/TM
WI = índice de trabajo del material en kwh/TM
P80 = tamaño de malla en micrones al cual pasa el 80 % del producto
F80 = tamaño de malla en micrones al cual pasa el 80 % de la alimentación

30. y la potencia del motor :
P= WF
donde F es la alimentación en TM/h

31. El índice de trabajo es el parámetro de conminución que expresa
la resistencia del material a ser fragmentado
Numéricamente corresponde a kwh por tonelada requerida para
reducir el material desde un tamaño de alimentación
teóricamente infinito hasta 80 % pasante la abertura de 100
micrones
Bond derivó ecuaciones para calcular el
índice de trabajo desde varios tipos de
pruebas de laboratorio :

32. Prueba de moliendabilidad en molino
de bolas
Se emplea el molino estándar de Bond de 12” x 12” con forros
pequeños y con las esquinas internas redondeadas. Gira a 70 rpm
El mineral es previamente triturado a – m 6 y se analiza por
tamaños

33. Se toma 700 cc de este mineral , se pesa y se coloca dentro del
molino . Se muele el mineral simulando una operación en circuito
cerrado con 250 % de carga circulante , empleando la carga de
bolas siguiente :
Diámetro de bola, N0 de bolas Peso en gramos
pulg
1,45 43 8803
1,17 67 7206
1 10 672
0,75 71 2011
0,61 94 1433
total 20 125

34.  La prueba se inicia moliendo el mineral por 100 revoluciones y
luego se descarga el molino y se tamiza con la malla de corte
requerida
 El pasante es pesado , se separa y es reemplazado por mineral
fresco hasta completar el peso inicial de carga y luego se carga
al molino
 Se reinicia la molienda por el numero de revoluciones
calculado para producir un 250 % de carga circulante , repitiendo
tal procedimiento hasta alcanzar las condiciones de equilibrio
 Luego de lograr el equilibrio, se tamiza el pasante con la malla
de corte
 El índice de trabajo se calcula :

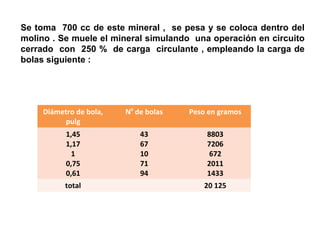
35. 49,1
WI = ---------------------------------------------------------
P10,23 Gbp0,82 [( 10 /√P 80 ) –( 10 / √F 80 ) ]
P1 es la abertura de la malla de corte empleada, en micrones
Gbp es la moliendabilidad en el molino de bolas y es el peso en
gramos del pasante producido por cada revolución

36. Ejemplo de una prueba de molienda
Se tomó 700 cc de mineral triturado - m 6 y el peso fue 910
gramos ( densidad aparente del mineral 1300 g/L)
El tamizaje de la alimentación dió F80 = 3025 micrómetros
Se usó la malla 270 como malla de corte
% en peso de - 53 µm en la alimentación = 8,2

37. Luego de las 100 revoluciones , se descargó el molino , tamizó y
se pesó el pasante , dando 171 gramos
- 53 µm en la alimentación = 910 x 0,082 = 74,6 g
Gbp = 96,4 gramos/100 rev = 0,964 g/rev
Se compensó la carga inicial, adicionando mineral fresco hasta
los 910 gramos
Se calculó la carga circulante = (739 / 171 ) 100
= 432 %

38. Con la carga de bolas y el mineral , se reinició la molienda
por 192 revoluciones (del cálculo con Gbp)
El peso del pasante la malla de corte fue 247 gramos
- 53 µm en la alimentación añadida = 171 x 0,082 = 14, 0
Gbp = 233 / 192 = 1,214
El porcentaje de carga circulante calculado : (663 /247) 100
: 268,4 %

39. Se requiere moler algo más y se repite la molienda esta vez por
203 revoluciones
El pasante pesó : 258,4 gramos
- 53 µm en la alimentación añadida = 258,4 x 0,082 = 21,2
Gbp = 237,2 /203 = 1,168
Carga circulante calculada = 252 %

40. Se repite la molienda , por 205 revoluciones
El peso del pasante fue : 260,2 gramos
- 53 µm en la alimentación añadida = 21,3 g
Gbp = 238,9 / 205 = 1,165
Carga circulante calculada = 249,7 %
Se tamizó el pasante la malla de corte

41. Resultados
P1 Gbp F80 P80
53 µm 1,182 3025 µm 46 µm
WI = 13,3 kwh/TM

42. Métodos indirectos de determinación del
índice de trabajo
Método de Berry y Bruce (1966)
 se prepara la muestra de mineral a 100 % - malla 10
 Se muelen 2 kg de muestra test con WI desconocido en el
molino de bolas estándar, bajo condiciones de molienda húmeda,
por un periodo de tiempo suficiente para alcanzar la finura del
mineral
 En condiciones idénticas al anterior, la muestra referencial de
WI conocido es molido

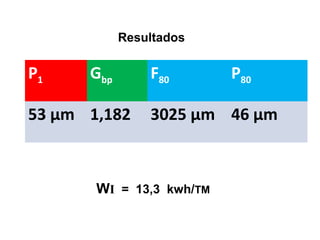
43.  Ambas muestras se tamizan para hallar el P80 y el F80
 La cantidad de energía consumida en ambos casos será similar
debido a que se han usado parámetros idénticos (porcentaje de
sólidos, carga de bolas, rpm, tiempo, etc.)
 Entonces, aplicando la Ley de Bond
W test = [WI (( 10 / √P80) – ( 10 / √F80))] test
W refer. = [WI (( 10 / √P80) – ( 10 / √F80))]ref

44.  Luego :
[( 10 / √P80) – ( 10 / √F80)]ref
WI test = WI
ref.
[( 10 / √P80) – ( 10 / √F80)] test