Este documento presenta una guía para el análisis y diseño estructural de edificios de hormigón armado. Explica conceptos fundamentales de ingeniería estructural como la modelación matemática de estructuras, cargas y condiciones de apoyo. También describe el proceso de análisis estructural que incluye la determinación de efectos de cargas, modelado en software de análisis y diseño de elementos estructurales. La guía provee información para la ingeniería estructural conceptual, análisis estático y dinámico,


















![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 14
2.8.1.2.8.1.2.8.1.2.8.1.---- Cargas sobre las VigasCargas sobre las VigasCargas sobre las VigasCargas sobre las Vigas
Viga del Eje C Nivel + 16.20 [Tn/m]
320.0CV
918.0CM
=
=
3.20
21
3
Sw
3
Sw
CM
×
+
×
=
3
Sw
3
Sw
CV
×
+
×
=
3
20.343.0
3
20.343.0
CM
×
+
×
=
3
20.315.0
3
20.315.0
CV
×
+
×
=
918.0CM = Tn/m 320.0CV = Tn/m
Viga del Eje C Nivel + 13.50 [Tn/m]
320.0CV
302.1CM
=
=
452.0CV
839.1CM
=
=
1 2 3
4.603.20
3
Sw
3
Sw
CM
×
+
×
=
3
Sw
2
m3
3
Sw
CM
2
×
+
−
×
×
=
3
20.361.0
3
20.361.0
CM
×
+
×
=
( )
3
60.461.0
2
847.03
3
90.361.0
CM
2
×
+
−
×
×
=
302.1CM = Tn/m 839.1CM = Tn/m
3
Sw
3
Sw
CV
×
+
×
=
3
Sw
2
m3
3
Sw
CV
2
×
+
−
×
×
=
3
20.315.0
3
20.315.0
CV
×
+
×
=
( )
3
60.415.0
2
847.03
3
90.315.0
CV
2
×
+
−
×
×
=
320.0CM = Tn/m 452.0CM = Tn/m](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-19-320.jpg)
![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 15
Viga del Eje C Nivel + 10.80, + 8.10, + 5.40, +2.70 [Tn/m]
320.0CV
898.1CM
=
=
452.0CV
685.2CM
=
=
1 2 3
4.603.20
3
Sw
3
Sw
CM
×
+
×
=
3
Sw
2
m3
3
Sw
CM
2
×
+
−
×
×
=
3
20.389.0
3
20.389.0
CM
×
+
×
=
( )
3
60.489.0
2
847.03
3
90.389.0
CM
2
×
+
−
×
×
=
898.1CM = Tn/m 685.2CM = Tn/m
3
Sw
3
Sw
CV
×
+
×
=
3
Sw
2
m3
3
Sw
CV
2
×
+
−
×
×
=
3
20.315.0
3
20.315.0
CV
×
+
×
=
( )
3
60.415.0
2
847.03
3
90.315.0
CV
2
×
+
−
×
×
=
320.0CM = Tn/m 452.0CM = Tn/m
Estas cargas distribuidas son las que se utilizarán en el pórtico para un análisis preliminar a la
definición de las secciones de la estructura. Para los otros pórticos que vamos a prediseñar
procedemos de la misma manera, como resultado cada pórtico deberá tener las solicitaciones por
carga muerta, por carga viva y por sismo, como se indica en los pórticos mostrados a continuación.](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-20-320.jpg)


![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 18
3.3.3.3.---- Opciones de Cálculo Estructural con el Programa Sap2000Opciones de Cálculo Estructural con el Programa Sap2000Opciones de Cálculo Estructural con el Programa Sap2000Opciones de Cálculo Estructural con el Programa Sap2000
Los cambios acordes a la actualidad en el contenido de los cursos de análisis y diseño estructural,
han venido eliminando algunos de los llamados “métodos clásicos” del análisis de estructuras los
cuales se pueden resolver “a mano” estructuras simples.
Estos cambios se llevan a cabo para poder dar énfasis a los “métodos modernos”, que se basan en
la resolución de los problemas mediante una herramienta computacional. Los cambios
tecnológicos en la educación en general y en ingeniería estructural son inevitables e irreversibles, y
dominar un programa computacional de resolución de estructuras ubica a los ingenieros a la
vanguardia.
Para esto un ingeniero estructural debe conocer las capacidades de solución numérica que ofrece el
paquete computacional; SAP 2000 permite realizar varios análisis, a continuación se detalla los
métodos de cálculo aplicados para resolver el problema y su solución.
3.1.3.1.3.1.3.1.---- Cálculo EstáticoCálculo EstáticoCálculo EstáticoCálculo Estático
El cálculo estático se ejecuta por defecto, a menos que se especifiquen parámetros dinámicos en la
Sección SYSTEM y se introduzca la masa dinámica, sea en la definición de los elementos o en la
Sección MASSES de masas concentradas, el problema estático se plantea en los siguientes términos:
[ ] [ ] [ ] m×nm×nn×n F=U×K
En donde:
n: Número de grados de libertad del sistema
m: Número de hipótesis de carga
K: Matriz de rigidez de la estructura
U: Vector de movimientos nodales, es matriz, si hay varias hipótesis de carga.
F: Vector de cargas, es matriz, si hay varias hipótesis de carga.
El programa construye la matriz de rigidez K de la estructura a partir de las matrices de rigidez
elementales, forma el vector o matriz de cargas estático F y resuelve el sistema de ecuaciones.
3.2.3.2.3.2.3.2.---- Cálculo DinámicoCálculo DinámicoCálculo DinámicoCálculo Dinámico
3.2.1.3.2.1.3.2.1.3.2.1.---- Análisis de Respuesta bajo Carga Sinusoidal.Análisis de Respuesta bajo Carga Sinusoidal.Análisis de Respuesta bajo Carga Sinusoidal.Análisis de Respuesta bajo Carga Sinusoidal.
Esta opción permite analizar un problema dinámico particular, el cálculo de la componente
estacionaria de la respuesta, cuando la carga varía sinusoidalmente con el tiempo y el
amortiguamiento estructural es nulo. La ecuación que define este problema será por lo tanto la
siguiente:
)wt(sen×F=)t(F=u×K+ü×M
En donde:
u: Vector de movimientos nodales
ü: Vector de aceleraciones nodales](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-23-320.jpg)
![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 19
M: Matriz de masas de la estructura
K: Matriz de rigidez de la estructura
F(t): Vector espacial de cargas que define las componentes de las acciones independientes del
tiempo.
Para un caso tan especial como éste, en el que la variación temporal de la carga dinámica es
sinusoidal y está concentrada en el término sen (wt) sin afectar al vector F, la solución es del tipo:
)wt(sen×U=u
donde U es un vector espacial de desplazamientos, cuyas componentes, al igual que en el vector F,
son independientes del tiempo.
La aceleración viene dada por la expresión:
)wt(senUwü 2
××=
Por tanto, el vector U lo obtendremos como solución al siguiente sistema de ecuaciones lineales;
[ ] F=U×M-w-K 2
El término w debe definirse Sección SYSTEM, a través de la frecuencia expresada en ciclos/seg.
Como se puede observar por lo expuesto anteriormente, este problema, aunque estrictamente es
de tipo dinámico, puesto que interviene la matriz de masa M, y la carga y la respuesta varían en el
tiempo, no lo es en el sentido de que es conocida la variación temporal de la componente
estacionaria de la respuesta, necesitando únicamente determinar su variación espacial. Por lo
tanto, la formulación resultante es de tipo estático, debiendo resolver un único sistema de
ecuaciones lineales, mientras que en un problema típico de integración directa de la ecuación
dinámica es necesario determinar previamente las frecuencias y modos propios y la precisión del
cálculo es proporcional al número de incrementos de tiempo.
3.2.2.3.2.2.3.2.2.3.2.2.---- Cálculo de Frecuencias y Modos de VibraciónCálculo de Frecuencias y Modos de VibraciónCálculo de Frecuencias y Modos de VibraciónCálculo de Frecuencias y Modos de Vibración
En la Sección SYSTEM se especifica el número de frecuencias y modos de vibración que se desea
calcular. La determinación de las frecuencias naturales es un requisito previo para cualquier otro
cálculo dinámico, como integración directa o análisis espectral. Como ya se ha comentado
anteriormente, el análisis de respuesta bajo carga sinusoidal es, a efectos de cálculo, equivalente a
un caso estático, no estando sujeto a este requisito previo.
Para los casos de integración directa y análisis espectral existe, como alternativa el cálculo de
frecuencias y modos propios, el uso de vectores de Ritz. Por otro lado, el cálculo de frecuencias y
modos propios puede ser de interés por sí solo, por el significado físico que tienen, sin necesidad
de recurrir a la integración directa de la ecuación dinámica para justificar su realización.
El programa utiliza un método de iteración de subespacios modificado, para obtener los períodos y
vectores propios de la estructura. La iteración de subespacios es un método muy utilizado para
resolver problemas de autovalores en grandes estructuras, cuando sólo interesa calcular un número](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-24-320.jpg)






























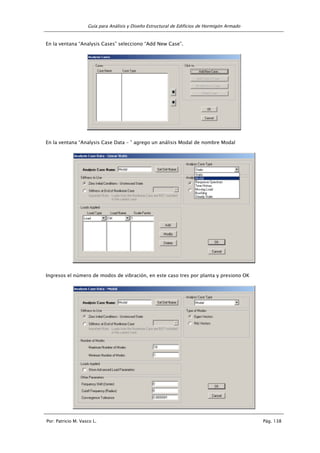
![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 54
-0.742
0.446
-0.757-0.266
0.128
-0.296
-0.262
0.122
-0.313 -0.761
0.460
-0.711
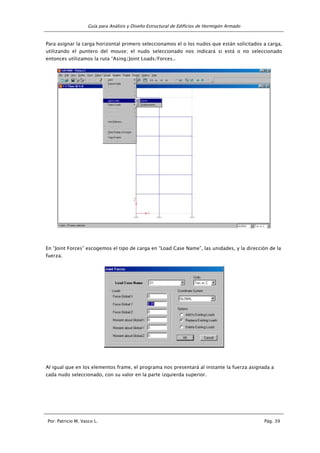
MOMENTOS POR CARGA VIVA [Kg-m]
-0.760
0.520
-0.591
0.454
-0.707-0.776
-0.669-0.790-0.372-0.212
0.118
-0.318-0.255
0.123
-0.399-0.220
0.100
0.466
0.231
-0.164
ESC :
PÓRTICO EJE C = EJE B
1 : 100
1 2 3
-0.194
3.20 4.59
2.70
2.70
2.70
2.70
2.70
2.70](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-59-320.jpg)
![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 55
-1.756
0.803
-1.880 -4.769
2.844
-4.540
321
1 : 100
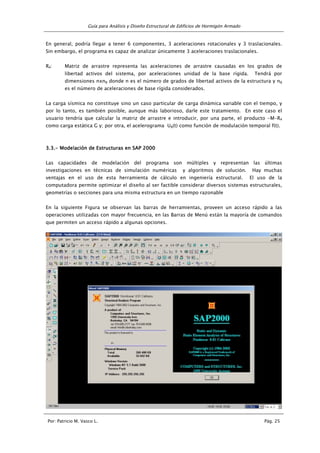
PÓRTICO EJE C = EJE B
ESC :
0.788
-1.654 -2.011 -4.448
2.870
-4.808
-1.348
0.760
-2.374 -4.972
2.921
-4.183
-1.606
0.791
-2.054 -4.889
2.848
-4.412
-1.089
0.499
-1.630 -3.283
2.252
-2.734
-0.551
0.770
-0.642
MOMENTOS POR CARGA MUERTA [Kg-m]
2.70
2.70
2.70
2.70
2.70
2.70
4.593.20](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-60-320.jpg)
![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 56
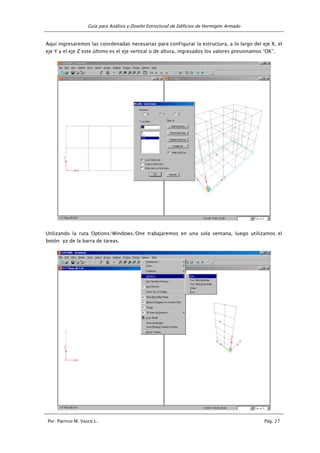
MOMENTOS POR CARGA DE SISMO [Kg-m]
-8.6459.476
-7.2726.345-8.4349.392
ESC :
PÓRTICO EJE C = EJE B
1 : 100
1 2 3
6.564 -7.354
7.601 -6.907 5.368 -6.011
-4.0003.598-4.4324.880
2.209 -1.967 1.806 -1.985
0.757 -0.850
3.20 4.59
2.70
2.70
2.70
2.70
2.70
2.70](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-61-320.jpg)
![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 57
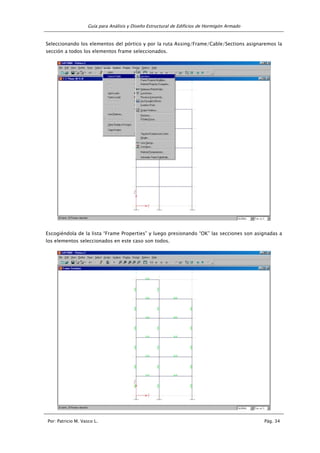
MOMENTOS POR COMBINACIONES DE CARGA [Kg-m]
-14.687
1.317
-15.303
-15.444
4.882
-15.128-14.796
1.264
-14.858
ESC :
PÓRTICO EJE C = EJE B
1 : 100
1 2 3
-15.330
4.759
-15.848
-12.732
1.311
-12.198 -13.547
4.800
-14.007
-11.319
4.740
-11.018-8.529
1.342
-9.066
-4.521
0.870
-4.978 -6.950
4.037
-6.408
-1.850
1.471
-2.111
3.20 4.59
2.70
2.70
2.70
2.70
2.70
2.70](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-62-320.jpg)





























































![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 120
9.9.9.9.---- Diseño en Hormigón ArmadoDiseño en Hormigón ArmadoDiseño en Hormigón ArmadoDiseño en Hormigón Armado
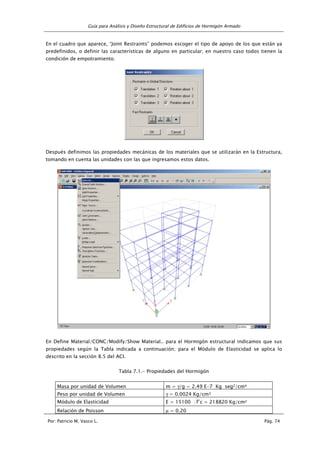
9.1.9.1.9.1.9.1.---- Diseño a FlexiónDiseño a FlexiónDiseño a FlexiónDiseño a Flexión
Secciones simplemente armadas.
C
T
d - a/2
a
c
0.85 f'cb
d
Equilibrio de Fuerzas
c'f85.0
fydρ
bc'f85.0
fyAs
a
fydbρfyAsabc'f85.0
TC
×
××
=
××
×
=
×××=×=×××
=
Equilibrio de Momentos
[ ]
×
××
−××××=
−×=
c'f
fy
85.0
dρ5.0
dfydbρMn
2
a
dTóCMn
El coeficiente de resistencia nominal K se obtienen cuando ambos lados de la ecuación se dividen
para 2
db × tenemos:
×
××
−××=
×
=
c'f85.0
fyρ5.0
1fyρ
db
Mn
K 2
La ecuación anterior puede usarse para determinar la porcentaje de acero ρ dado un valor Mu o
vice-versa si las propiedades de la sección b y d son conocidas. Sustituyendo Mn= Mu/ø en la
ecuación (3) y dividiendo todo para f´c tenemos:
×
××
−
×
=
××× c'f85.0
fyp5.0
1
c'f
fyρ
dbc'fø
Mu
2
ɛc
ɛs](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-125-320.jpg)

![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 122
Si el acero no Fluye calculo c
0
1βbc'f85.0
'd'As6100
c
1βbc'f85.0
fyAs'As6100
c2
=
×××
××
−
×××
×−×
+
−×=
c
'd
16100fs
)'dd('fs'As)2/ad(bac`f85.0Mn −××+−××××=
)'dd('fs'As)2/ad(bac`f85.0øMu −××+−×××××=
Para todas las secciones rectangulares la resistencia de diseño øMn debe ser igual o mayor que el
esfuerzo requerido Mu. Además, los requisitos de servicio para deflexiones deben controlarse con
ACI 318-99 sección 9.5 y la distribución de refuerzo debe cumplir lo especificado en ACI 318-99
sección 10.6.
Reportes para Diseño Viga del Eje C Nivel + 16.20 [Tn-m]
-5.24 -4.87
3.20
21
Asumo un porcentaje de acero que puede ser menor o igual que el máximo:
016.0ρmáx =
Calculo el índice de refuerzo para ese porcentaje y obtengo:
c'f
fy
ρq máxmáx ×= 320.0qmáx =
Calculo el Momento Último Resistente para le sección de la Viga.
)q59.01(dbc'fqøMu 2
w ×−×××××=
)32.059.01(222521032.09.0Mu 2
×−×××××=
cmKg65.593642Mu −=
mTn95.5Mu −=
0.53](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-127-320.jpg)
![Guía para Análisis y Diseño Estructural de Edificios de Hormigón Armado
Por: Patricio M. Vasco L. Pág. 123
Comparo el Momento Resistente con el Momento Solicitante para la viga
Mu > Ms
5.95 > 5.24 [Tn-m]
Viga Rectangular Simplemente Armada
Calculo la constante K para calcular el porcentaje de acero en la sección
2
dbc'fø
Mu
K
×××
=
2
5
22252109.0
1024.5
K
×××
×
=
229.0K = 424.0Kmax =
Calculo el porcentaje de acero, este debe ser menor que el máximo permitido y mayor que
el mínimo.
18.1
K36.211
fy
c´f
ρ
×−−
×=
18.1
229.036.211
4200
210
ρ
×−−
×=
014.0ρ =
0033.0ρmin = 016.0ρmáx =
014.0ρ =
Calculo el Área de Acero en la sección
dbρAs ××=
2225014.0As ××=
2
cm70.7As =](https://image.slidesharecdn.com/2diseoedificio-sap2000-140725163604-phpapp02/85/2-diseno-edificio-sap2000-128-320.jpg)