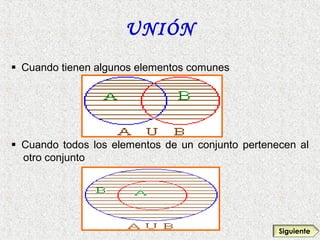
Este documento presenta los fundamentos de la teoría de conjuntos, incluyendo la definición de conjuntos y elementos, la notación de conjuntos, las formas de determinar conjuntos, la clasificación de conjuntos, la representación gráfica de conjuntos a través de diagramas de Venn y Euler, y las operaciones básicas con conjuntos como la unión, intersección, diferencia y complemento.

1. FUNDAMENTOS DE LA TEORÍA DE
CONJUNTOS
Definición de
Conjuntos
Notación de
Conjuntos
Determinación de
Conjuntos
Clasificación de
Conjuntos
Representación gráfica de
conjuntos- Diagramas de Venn –
Euler.
Igualdad de
Conjuntos
Operaciones con
Conjuntos
Siguiente

2. DEFINICIÓN DE CONJUNTO
 Conjunto: Es una agrupación o colección bien definida de objetos,
donde cada objeto es un elemento o miembro del conjunto que
satisfacen ciertas propiedades específicas.
 Elemento: Llamaremos elemento, a cada uno de los objetos que forman
parte de un conjunto, estos elementos tienen carácter individual, tienen
cualidades que nos permiten diferenciarlos, y cada uno de ellos es
único, no habiendo elementos duplicados o repetidos.
Siguiente

3. NOTACIÓN DE LA TEORÍA DE
CONJUNTOS
 Conjunto: Se denota con una letra mayúscula: A, B, C, o
enumerando sus elementos separados por comas y
delimitándolos por llaves: { }
 Elementos: Se denotan con letras minúsculas: a, b, c, d, a
menos que dichos elementos sean a su vez conjuntos.
 Relación de pertenencia: Sea x un elemento cualquiera y
A un conjunto. Si es cierto que x es un elemento de A, se
dice que x pertenece a A y se denota: x ∈A.
 (∈ : Letra griega epsilón)
 Relación de no pertenencia: Si no es cierto que x es un
elemento de A, se dice que x no pertenece a A y se denota
como: x ∉ A. Siguiente

4. DETERMINACIÓN DE
CONJUNTO
Hay dos formas de determinar conjuntos, por extensión y
por comprensión:
 Por extensión: Se dice que un conjunto es
determinado por extensión (o enumeración), cuando se
da una lista que comprende a todos los elementos del
conjunto y sólo a ellos. En un conjunto determinado por
extensión no se repite un mismo elemento.
 Ejemplo:
 B = { 2, 4, 6, 8 }
 C = { c, o, n, j, u, t, s }
 A = { 7,2,8,5,3,23} Siguiente

5. DETERMINACIÓN DE
CONJUNTO
 Por comprensión o forma constructiva: Se dice que un
conjunto es determinado por comprensión, cuando se da
una propiedad que la cumpla en todos los elementos del
conjunto y sólo a ellos. Este implica usar la notación
siguiente para determinar un conjunto dado A.
A = { x tal que x es un objeto que verifica una condición dada }
O en forma más simple:
A = { x / x es un objeto que verifica una condición dada }
 Ejemplos:
B = { x / x es un número par menor que 10 }
C = { x / x es una letra de la palabra conjunto }
D = { x / x ∈ N 0< x ≤5 } Siguiente

6. REPRESENTACIÓN GRÁFICA
DEL CONJUNTO
 Diagramas de Venn: Son esquemas que nos permiten hacer la
representación grafica de los conjuntos. A cada conjunto se le
considera encerrado dentro de una curva (plana) cerrada. Los
elementos del conjunto considerado pueden ser
específicamente dibujados o pueden quedar (implícitamente)
sobreentendidos. Los diagramas son empleados, para
representar tanto a los conjuntos como a sus operaciones, y
constituyen una poderosa herramienta geométrica, desprovista
de validez lógica.
El conjunto universo U, se representa por un rectángulo o por
un cuadrado.
Siguiente

7.  Los conjuntos que se encuentran en el universo, se
representan por líneas curvas cerradas que demarcan los
elementos del conjunto.
REPRESENTACIÓN GRÁFICA
DE CONJUNTO
Siguiente

8. IGUALDAD DE CONJUNTOS
 Se dice que dos conjuntos A y B son iguales cuando
ambos tienen los mismos elementos, es decir si cada
elemento de A pertenece a B y si cada elemento que
pertenece a B pertenece también a A. La igualdad se
denota A = B. En la igualdad, el orden de los elementos de
cada conjunto no importa.
 Ejemplos:
A = {1, 2, 3, 4} y B = {3, 4, 1, 2} entonces A = B
C = {1, 2, 3, 3, 4, 1} y D = 1, 2, 2, 3, 4, 4} entonces C = D
E = {x/x son vocales de la palabra mundo} y F = {u, o }
entonces E = F
Siguiente

9.  Sean A y B dos conjuntos tal que todo elemento de A es
también elemento de B, entonces decimos que:
 A es un subconjunto de B.
 A es una parte de B
 A está incluido en B
Se denota o simboliza A B.
Su definición matemática es: A B x A x B⇔∀
RELACIÓN DE CONTENIDO Ó
SUBCONJUNTO Ó INCLUSIÓN
∈ ⇒∈⊂
⊂
Siguiente

10. INCLUSIÓN DE CONJUNTOS
 Ejemplos:
  Dados los conjuntos
  A = { 0 , 3 }
  B = { 0,1,2,3,4, }
Observe
  A ⊂ B porque 0 y 3 ∈ B
  B ⊄ A porque 1,2 y 4 ∉ A
.
Siguiente

11. OPERACIONES CON
CONJUNTOS
 Unión de conjuntos: La unión de los conjuntos A y B es el
conjunto formado por todos los elementos que pertenecen
al conjunto A o al conjunto B o a ambos. Se denota: A U B.
La unión de conjuntos se define como:
 A U B = {x / x ∈ A ∨ x ∈ B }.
Mediante un diagrama de Venn-Euler
 Cuando no tienen elementos comunes
Siguiente

12. UNIÓN
 Cuando tienen algunos elementos comunes
 Cuando todos los elementos de un conjunto pertenecen al
otro conjunto
Siguiente

13. INTERSECCIÓN
 Se define la intersección de dos conjuntos A y B al conjunto
de elementos que son comunes en el conjunto A y en el
conjunto B. Se denota por A B, que se lee: A intersección B.
También se puede definir:
 A B = { x / x ∈ A ∧ x ∈ B }.
Mediante un diagrama de Venn-Euler
  Cuando no tienen elementos comunes
Siguiente

14. INTERSECCIÓN
  Cuando tienen elementos comunes
 Cuando todos los elementos de un conjunto pertenecen al
otro conjunto
Siguiente

15. DIFERENCIA
Se denomina diferencia de dos conjuntos A y B al conjunto
formado por todos los elementos de A pero que no
pertenecen a B.
La diferencia se denota por: A – B que se lee: A diferencia B o
A menos B.
Se define la diferencia de dos conjuntos también como:
A – B = {x / x ∈ A ∧ x ∉ B }.
Mediante un diagrama de Venn-Euler
Cuando no tienen elementos comunes
Siguiente

16. DIFERENCIA
 Cuando tienen elementos comunes
 Cuando todos los elementos de un conjunto pertenecen al
otro conjunto
Siguiente

17. COMPLEMENTO
 Para cualquier conjunto A, tal que ACU, el complemento de
A, denotado por AC
, A', se define como el conjunto de los
elementos que pertenecen a U y no pertenecen al conjunto
A.
 Simbólicamente se expresa: AC
= U-A ={ x/ x ∈ U ∧ x ∉ A}
 Mediante un diagrama de Venn-Euler
Siguiente

18. DIFERENCIA SIMETRICA
 Es el conjunto formado por los elementos
que pertenecen a la unión de los conjuntos
exceptuando la intersección.
 A B ={ x / x ∈ (AUB) ∧ x ∉ (A B) }