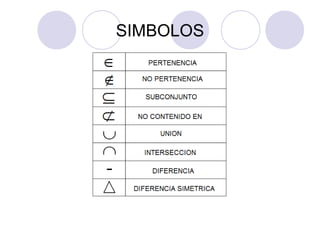
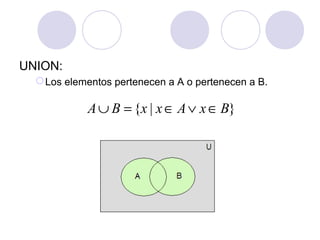
Este documento presenta los conceptos básicos de la teoría de conjuntos. Define un conjunto como una colección de objetos bien definidos y diferenciables llamados elementos. Explica formas de definir conjuntos, operaciones entre conjuntos como la unión e intersección, y conceptos como el subconjunto, complemento y cardinalidad. También describe la relación entre la teoría de conjuntos y la lógica proposicional.

1. TEORIA DE CONJUNTOS
CORPORACION
UNIVERSITARIA AMERICANA

2. CONJUNTO
Un conjunto es la reunión en un todo de
objetos bien definidos y diferenciables entre
si, que reciben el nombre de elementos.
Los conjuntos son representados por letras
mayúsculas (A, B, C, …) y los elementos
por letras minúsculas (a, b, c, …).

3. DEFINICION DE CONJUNTO
Se puede definir un conjunto por:
Extensión: En el cual se enumeran todos y
cada uno de sus elementos.
Compresión: En el cuál se da la propiedad que
caracteriza a los elementos que lo conforman.

4. Un conjunto se escribe encerrando entre
llaves, los elementos que lo conforman:
A={1,2,3,…}
B={n є Z | p es par}

5. Ejemplo:
Conjunto por extensión
A = {2,4,6,8,10,12,14,16,18,20}
Conjunto por compresión
A = { x | x es par}

6. SIMBOLOS

7. DIAGRAMA DE VENN-EULER
Es la representación gráfica
de los conjuntos, donde el
conjunto referencial se dibuja
como un rectángulo y los
demás conjuntos
(subconjuntos) se grafican
con círculos contenidos en el
rectángulo.

8. CONSTRUCCION DE CONJUNTOS
Si U={1,2,3,4,5,6} representa los posibles
resultados al lanzar un dado; un jugador A
gana cuando al lanzar el dado saca más de
2 y un jugador B gana si el resultado es par.

9. Para el jugador A: A = { x | x > 2} = {3,4,5,6}
Para el jugador B: B = { x | x es par} = {2,4,6}

10. COMPLEMENTO DE UN CONJUNTO
El conjunto de elementos que no cumplan con la
propiedad establecida, se denomina
“complemento” y se indica con una “C” en la parte
superior derecha de la letra que representa el
conjunto analizado.
Aͨ = { Ïx | x A }

11. Continuación del Ejemplo:
Para el jugador A: A = { x | x > 2} = {3,4,5,6}
Para el jugador B: B = { x | x es par} = {2,4,6}
En éste caso, el complemento corresponde al
conjunto de elementos con el que los
jugadores pierden.

12. Continuación del Ejemplo:
U = { 1,2,3,4,5,6 }
A = { x | x > 2} = {3,4,5,6}
Aͨ = { x | x ≤ 2} = { 1,2 }
B = { x | x es par} = {2,4,6}
Bͨ = { x | x no es par} = { 1,3,5 }

13. NOTA: Si una propiedad no es cumplida por
ningún elemento del conjunto general, se llama a
este conjunto “vacío”.
{ } = Æ

14. Relaciones
de Contenencia e Igualdad
Si se tiene dos conjuntos (A, B) y se establece
que “todo elemento de A es elemento de B” se
dice que A es un subconjunto de B y se escribe:
A Í B
Si A no está contenido en B se escribe:
A Ë B

15. Ejemplo:
Dados A = {1,2,3,4}; B = {1,2,3,4,5}; C
= {2,3,4,6}

16. Ejemplo:
Dados A = {1,2,3,4}; B = {1,2,3,4,5}; C = {2,3,4,6}
A Í B
A Ë C

17. OPERACIONES ENTRE CONJUNTOS
INTERSECCION:
AÇB = {x | xÎ A Ù xÎB}
Intersección entre A y B:

18. CONJUNTO VACIO:
Cuando no hay elementos en común entre los dos
conjuntos, se dice que son conjuntos “disyuntos”
AÇB =Æ

19. UNION:
Los elementos pertenecen a A o pertenecen a B.
AÈB = {x | xÎ AÚ xÎB}

20. DIFERENCIA:
Se da cuando los elementos que pertenecen a un
conjunto, NO pertenecen a otro conjunto.
A- B = {x | xÎ AÙ xÏB}

21. DIFERENCIA SIMETRICA:
Es cuando los elementos están en uno u otro conjunto,
pero no en ambos.
ADB = {x | xÎ(AÈB) Ù xÏ(AÇB)}

22. Ejemplo:
Dados los conjuntos:
U = {0,1,2,3,4,5,6,7,8,9,10,11,12}
A = {0,2,4,6,8,10,12}
B = {1,2,3,4,5,6}
C = {4,5,6,7,8,9}
Ejecutar: AÈB
C - A
AÇB
ACDC

23. Solución:
AÈB
AÈB
Ejecutar:
A = {0,2,4,6,8,10,12}
B = {1,2,3,4,5,6}
 = {0,1,2,3,4,5,6,8,10,12}

24. Solución:
C - A
C - A
Ejecutar:
A = {0,2,4,6,8,10,12}
C = {4,5,6,7,8,9}
 = {5,7,9}

25. Solución:
AÇB
AÇB
Ejecutar:
A = {0,2,4,6,8,10,12}
B = {1,2,3,4,5,6}
 = {2,4,6}

26. Solución:ACDC
Ejecutar:
A = {0,2,4,6,8,10,12}  Aͨ = {1,3,5,7,9,11}
C = {4,5,6,7,8,9}
 A C D C = {1,3,4,6,8,11}

27. Ejercicio:
Dados U = {0,1,2,3,4,5,6,7,8,9}
A = { x | x < 6}
.
.
B = {x | 3 £ x < 9}
C = {x | x £ 3 ó x ³ 8}
Efectuar:
A È
B
A Ç
C
A D (C -
Ac )

28. PERTENENCIA ó NO PERTENENCIA
Si a es un elemento del conjunto A se denota con
la relación de pertenencia a ϵ A.
En caso contrario, si a no es un elemento de A se
denota a ϵ A.
Ejemplo: Diga si los siguientes números pertenecen ó
pertenecen al conjunto A.
1,3,8,10
A = {1,2,5,6,8,9,11,12,14,15}

29. A
A
A
A
Î
Ï
Î
Ï
1
3
8
10

30. Se llama unión de dos conjuntos A y B al conjunto
formado por objetos que son elementos de A o de
B,
es decir:
AÈB ={x | xÎ AÚ xÎB}
Se llama intersección de dos conjuntos A y B al
conjunto formado por objetos que son elementos
de A y de B, es decir:
AÇB ={x | xÎ AÙ xÎB}

31. RELACION ENTRE LA TEORIA DE
CONJUNTOS Y LA LOGICA PROPOSICIONAL
Existe una relación muy estrecha entre la Teoría
de Conjuntos y la Lógica Proposicional.
Para mostrar dicha relación, denotemos por letras
mayúsculas A,B ... los conjuntos y
por las correspondientes minúsculas a,b ... sus
propiedades características
(es decir, la proposición lógica que caracteriza a
los elementos de cada conjunto).

33. Además, el conjunto vacío se corresponde con
una contradicción y el conjunto universal con una
tautología.
Mediante esta correspondencia, todos los
resultados sobre conjuntos se pueden rescribir en
términos de lógica
proposicional y viceversa; a modo de ejemplo:

35. CARDINALIDAD DE CONJUNTOS
La cardinalidad de un conjunto se define como la
cantidad de elementos que contiene dicho
conjunto y se denota por n(X).
En el caso de un conjunto P = {Planetas del
sistema solar}, su cardinalidad es: n(P) = 9, pues
el número de planetas que tiene el sistema solar
es nueve.

36. Los siguientes conjuntos se definen en
función de su cardinalidad:

37. 1. CONJUNTOS FINITOS E INFINITOS
Se les llama conjuntos finitos aquellos conjuntos
cuyos elementos se pueden contar, no importando
la dificultad que ello represente; por ejemplo:
A = {letras vocales}
B = {meses del año}
C = {xÎN | 5 < x < 20}

38. Los conjuntos infinitos son aquellos que tienen un
número ilimitado de elementos (no se pueden
contar); por ejemplo:
N = {Números naturales}
Z = {Números Enteros}
Q = {Números Racionales}
los elementos de estos tres conjuntos no se
pueden contar, pues no existe un número natural
último, siempre existirá uno mayor.

39. 2. CONJUNTO UNIVERSAL
Es el conjunto que contiene a la totalidad de los elementos
que intervienen en una discusión o situación particular. Por
ejemplo, en el caso de nuestro ejemplo, P = {planetas del
sistema solar}, el conjunto universal es U = {x | x es un
cuerpo celeste}.
En aritmética, podemos considerar al conjunto universal,
como el conjunto de todos los números reales, y de ahí,
podemos estudiar subconjuntos tales como, los números
naturales, los números enteros, los números racionales y
los números irracionales.

40. 3. CONJUNTO VACIO
Se define como conjunto vacío, al conjunto que
no tiene elementos, y se le denota como Æ

41. 4. CONJUNTOS EQUIVALENTES( ®
)
Dos conjuntos son equivalentes si puede
establecerse una correspondencia biunívoca
entre sus elementos, es decir, si ambos tienen el
mismo número de elementos.

42. 5. CONJUNTOS IGUALES (=)
Dos conjuntos son iguales si tienen
exactamente los mismos elementos, no
importa si éstos aparecen en diferente
orden en ambos conjuntos, o si los
conjuntos se escriben en formas diferentes,
por ejemplo:
{ los números enteros mayores que 3 y menores que 8} = {4,
5, 6, 7}

43. PROPOSICIONES CON
CUANTIFICADORES
 (1) Cuantificador universal ( ):
"xÎ A® p(x)
 se lee "para todo x que pertenece a A se verifica p(x)", representa
la proposición
 (2) Cuantificador existencial ( ):
$xÎ A| p(x)
 se lee "existe x que pertenece a A tal que p(x)", representa la
proposición