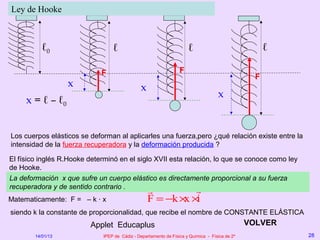
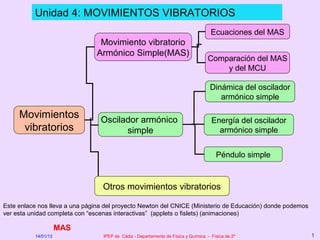
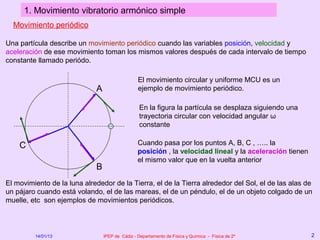
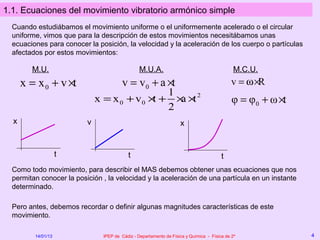
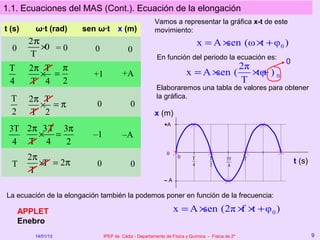
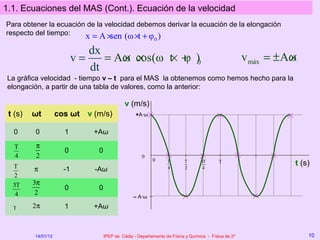
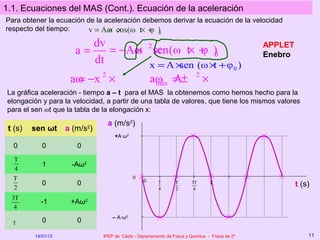
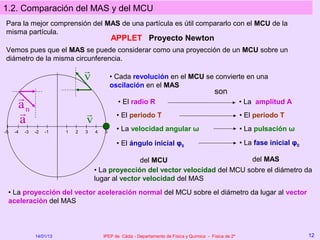
Este documento describe el movimiento vibratorio armónico simple (MAS), incluyendo sus ecuaciones, parámetros y comparación con el movimiento circular uniforme. Explica que el MAS es un movimiento periódico donde la posición sigue una función senoidal y la velocidad y aceleración también varían de forma periódica. Compara el MAS con el MCU, notando que el MAS es efectivamente una proyección del MCU sobre un diámetro.













![2.2. Energía del Oscilador armónico simple
Hemos visto que un oscilador armónico es un sistema material que se mueve con movimiento
armónico simple MAS.
La energía mecánica que posee es CINÉTICA, porque está en movimiento y POTENCIAL
ELÁSTICA, ya que el movimiento armónico es consecuencia de la acción de una fuerza
conservativa (la fuerza elástica recuperadora).
Energía cinética
La partícula de masa m que se mueve con una velocidad v tendrá una energía cinética:
1
Ec = × × 2
m v
2
Recordando la ecuación de la velocidad y la expresión de la constante k:
1
v = Aω cos(ω t× + )
× × m [
v 2 cos(ωt + φ0 )]
2
φ 0 Ec = × × Aω ×
2
1
kω m×
= 2 Ec = × × 2 2 cos 2
m Aω × (ωt + 0 φ )
2
1
Ec = × × 2 × 2 (ωt + φ 0 )
k A cos
2
1 1 1
Ec = × × 2 × −sen 2 (ωt + φ 0 )] = × × 2 − × × 22 sen 2 (ωt + φ 0 )
k A [1 k A k A
x
2 2 2
1
Ec = × × 2 − x 2 )
k (A
2
14/01/13 IPEP de Cádiz - Departamento de Física y Química - Física de 2º 21](https://image.slidesharecdn.com/2f02amovimientosvibratorios-130114120125-phpapp01/85/2f-02-a-movimientos-vibratorios-21-320.jpg)