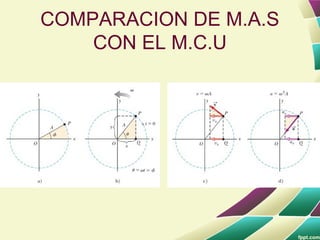
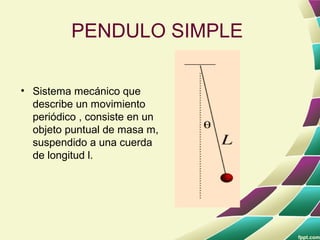
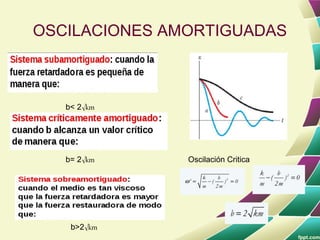
Este documento trata sobre el movimiento oscilatorio y el movimiento armónico simple. Explica conceptos como amplitud, periodo, frecuencia, posición de equilibrio, ley de Hooke, representación matemática, energía, velocidad y aceleración en el movimiento armónico simple. También compara el movimiento armónico simple con otros tipos de movimiento y analiza el pendulo simple, pendulo físico, oscilaciones amortiguadas y oscilaciones forzadas.

1. UNIVERSIDAD TECNICA PARTICULAR DE LOJA
INTEGRANTES:
Paola Arévalo
Luis Loján
Carlos Vivanco

2. MOVIMIENTO OSCILATORIO

3. El movimiento oscilatorio es aquel en el que el objeto retorna regularmente
a una posición dada en intervalos fijos de tiempo.

4. MOVIMIENTO ARMONICO
SIMPLE
• El movimiento armónico simple, también denominado
movimiento vibratorio armónico simple es un movimiento
rectilíneo con aceleración variable producido por las
fuerzas que se originan cuando un cuerpo se separa de
su posición de equilibrio, ejemplo el péndulo de
un reloj o una masa suspendida de un resorte.

5. Movimiento de un cuerpo unido
a un resorte
• Un bloque de masa m esta
atado a un resorte, el bloque
puede moverse sin fricción
sobre una superficie
horizontal.
• Cuando el resorte no esta ni
comprimido ni estirado el
bloque esta en su posición de
equilibrio.
• X=0

6. LEY DE HOOKE
• Establece que: Fs= -KX
 FS : es una fuerza restauradora
• esta siempre dirigida hacia la posición de equilibrio .
• siempre dirigida en sentido contrario al desplazamiento.
 K es la constante del resorte
 X es el desplazamiento
ACELERACION
•SEGUNDA LEY DE NEWTON:
F=ma F= -kx
-kx=ma

7. Representación matemática
del MAS
Sea: y entonces
A es la amplitud del movimiento
ω es la frecuencia angular
Φoδ contante de fase o ángulo inicial
(ωt+ Φ) es la fase

8. MOVIMIENTO ARMONICO SIMPLE
• ELEMENTOS:
» Oscilación
» Elongación
» Amplitud
» Periodo
» Frecuencia
» Posición de equilibrio

9. • Es el tiempo que tarda la partícula
PERIODO (T) en realizar una oscilación completa.
Esto ocurre cuando pasa dos veces
consecutivas por la misma posición
y en el mismo sentido del
movimiento.
FRECUENCIA (f) •Es el inverso de l período.
•Numero de oscilaciones en la unidad de
tiempo.

10. VELOCIDAD Y ACELERACION
M.A.S
•El desplazamiento, la velocidad y la aceleración varían
senoidalmente con el tiempo, pero no están en fase.
•La aceleración de la partícula es proporcional al desplazamiento,
pero tiene la dirección opuesta.
• La frecuencia y el periodo del movimiento son independientes de
la amplitud.

11. ENERGIA DEL OSCILADOR
ARMONICO SIMPLE
• Toda partícula sometida a un movimiento
armónico simple posee una energía
mecánica que podemos descomponer en:
Energía Cinética (debida a que la
partícula está en movimiento) y Energía
Potencial (debida a que el movimiento
armónico es producido por una fuerza
conservativa).

12. ENERGIA DEL OSCILADOR
ARMONICO SIMPLE

13. Velocidad como función para la
posición de un oscilador en
M.A.S

14. COMPARACION DE M.A.S
CON EL M.C.U

15. COMPARACION DE M.A.S
CON EL M.C.U

16. PENDULO SIMPLE
• Sistema mecánico que
describe un movimiento
periódico , consiste en un
objeto puntual de masa m,
suspendido a una cuerda
de longitud l.

17. PENDULO SIMPLE
•Actúa el P y la T.
•Las componentes del P: radial m.g.cos θ y
tangencial m.g.sen θ.

18. PENDULO FISICO
Un péndulo compuesto o físico es
cualquier cuerpo rígido que puede oscilar
libremente alrededor de un eje horizontal,
que no pasa por su centro de masa.

19. PENDULO FISICO

20. OSCILACIONES AMORTIGUADAS
• La disminución de la amplitud causada por fuerzas
disipadoras se denomina amortiguamiento y el
movimiento correspondiente se llama oscilación.
• Sobre un cuerpo actúa una fuerza adicional debido a
la fricción Fx= -bv .
Frecuencia natural
SEGUNDA LEY DE NEWTON

21. OSCILACIONOES AMORTIGUADAS
• Si la fuerza de amortiguamiento en relativamente pequeña, el
movimiento esta descrito por:
La frecuencia angular de la
oscilación es:

22. OSCILACIONES AMORTIGUADAS
b< 2√km
b= 2√km Oscilación Critica
b>2√km

23. OSCILACIONES FORZADAS
• Si aplicamos una fuerza
impulsora que varié
periódicamente con
frecuencia angular w a un
oscilador armónico
amortiguado, el movimiento
resultante se llama
oscilación forzada.
• w Frecuencia angular
impulsora.

24. OSCILACIONES FORZADAS