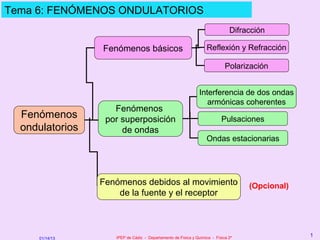
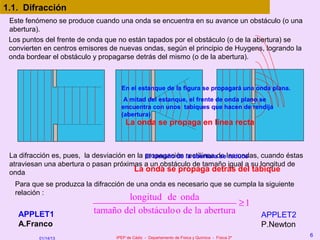
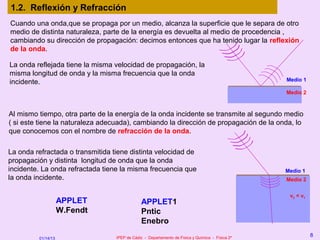
Este documento resume los principales fenómenos ondulatorios como la difracción, reflexión, refracción y polarización. Explica el principio de Huygens para la interpretación de estos fenómenos. También describe los fenómenos de interferencia que ocurren cuando dos ondas se superponen, incluyendo las ondas estacionarias resultantes de la interferencia de ondas que se propagan en sentidos opuestos.






















![Interferencia (Detalle)
y 2 = A × (ω ×t − k ×d 2 )
sen
P
d1 y1 = A × (ω ×t − k ×d1 )
sen
Según el principio de superposición, la elongación y
resultante será:
Foco 1 d2 y r = y1 + y 2 = A ×sen (ω ×t − k ×d1 ) + A ×sen (ω ×t − k ×d 2 )
Sacamos factor común A :
y r = A × sen (ω ×t − k ×d1 ) + sen (ω ×t − k ×d 2 ) ] =
[
Foco 2
(ω ×t − k ×d1 ) + (ω ×t − k × 2 )
d (ω ×t − k × 1 ) − (ω ×t − k ×d 2 )
d
= 2A ×
sen ×cos
2 2
A+B A−B
sen A + sen B = 2 ×sen ×cos
2 2
d 2 − d1 d 2 + d1 )
y r = 2A ×cos k ÷ × t× −
senω k ÷
Movimiento ondulatorio de la misma frecuencia y
longitud de onda que los movimientos que
2 2 interfieren y cuya amplitud y fase dependen de
las distancias d1 y d2 a los focos emisores.
y r = A r × (ω ×t − k ×x)
sen
Sigue
IPEP de Cádiz - Departamento de Física y Química - Física 2º
30
01/14/13](https://image.slidesharecdn.com/2f02cfenomenosondulatorios-130114120531-phpapp02/85/2f-02-c-fenomenos-ondulatorios-30-320.jpg)

![Ondas estacionarias (Detalle)
y r = y1 + y 2 = A ×sen (ω ×t − k ×x) + A ×sen (ω ×t + k ×x)
Sacamos factor común A :
y r = A × sen (ω ×t − kx) + sen (ω ×t + k ×x) ] =
[
(ω ×t − kx) + (ω ×t + k ×x) (ω ×t − kx) − (ω ×t + k ×x)
y r = 2A ×
sen ×cos
2 2
A+B A−B
sen A + sen B = 2 ×sen ×cos
2 2
y r = 2A ×cos (−kx) × (ω ×t) = 2A ×cos (kx) × (ω ×t)
sen sen Ecuación de la
onda estacionaria
y r = A r ×sen (ω ×t)
A r = 2A ×cos (k ×x)
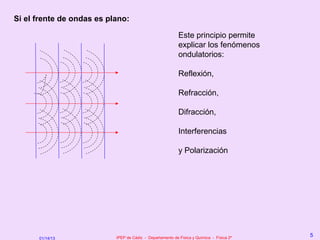
La onda estacionaria es armónica, de igual frecuencia que las componentes y con una
amplitud A que es independiente del tiempo, pero que varía sinusoidalmente con la abcisa x.
● Hay puntos cuya amplitud Ar es nula Son los NODOS (no oscilan)
● Hay puntos cuya amplitud Ar es máxima Son los VIENTRES o ANTINODOS
Sigue
IPEP de Cádiz - Departamento de Física y Química - Física 2º
32
01/14/13](https://image.slidesharecdn.com/2f02cfenomenosondulatorios-130114120531-phpapp02/85/2f-02-c-fenomenos-ondulatorios-32-320.jpg)
![Ondas estacionarias (Detalle)
¿Qué posición ocupan los vientres y los nodos? y r = 2A ×cos (kx) × (ω ×t)
sen
La amplitud de cada punto nos viene dada por la expresión: A r = 2A ×cos (k ×x)
● La amplitud Ar será máxima ( 2 A ) cuando:
nπ nπ λ
cos ( k x ) = ±1 k x = nπ x= x= x=n
k 2π 2
n = 0, 1 , 2 , 3 , …
λ
Serán vientres todos aquellos puntos cuya distancia a un foco vale un número entero de
semilongitudes de onda.
● La amplitud Ar será nula cuando: (2n + 1)π
π (2n + 1)π λ
cos ( k x ) = 0 k x = (2n + 1) x= x= x = (2n + 1)
2 2k 2π 4
n = 0, 1 , 2 , 3 , … 2
λ
Serán nodos todos aquellos puntos cuya distancia a un foco vale un número impar de
cuartos de longitudes de onda.
Distancia entre dos nodos consecutivos o dos vientres consecutivos es media longitud de onda:
λ λ λ λ λ λ
● Entre vientres: x n − x n −1 = n −(n − 1) = n − n + =
2 2 2 2 2 2
λ λ λ λ λ
● Entre nodos: x n − x n −1 = (2n + 1) − [ 2(n − 1) + 1] = (2n + 1 − 2n + 2 − 1) = 2 =
4 4 4 4 2
En consecuencia, la distancia entre un vientre y un nodo es de un cuarto de longitud de onda:
N N V
V λ
Volver
4 33
01/14/13 IPEP de Cádiz - Departamento de Física y Química - Física 2º](https://image.slidesharecdn.com/2f02cfenomenosondulatorios-130114120531-phpapp02/85/2f-02-c-fenomenos-ondulatorios-33-320.jpg)
