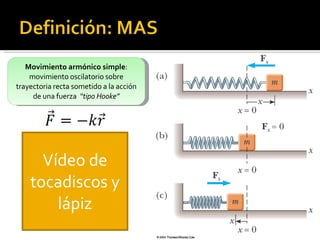
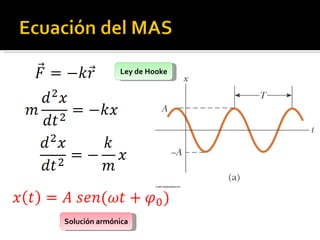
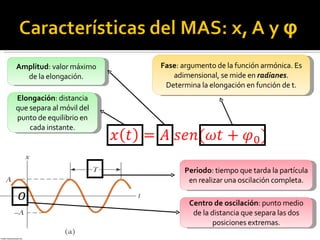
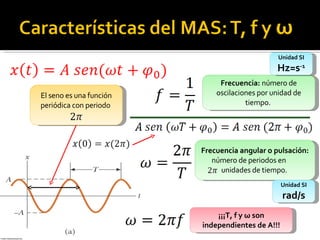
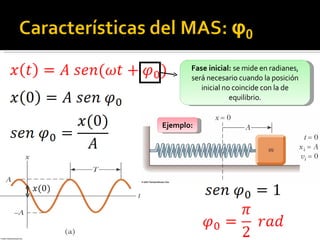
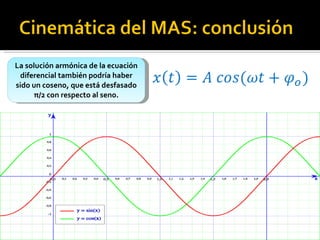
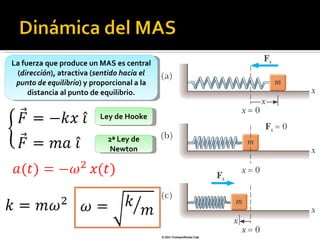
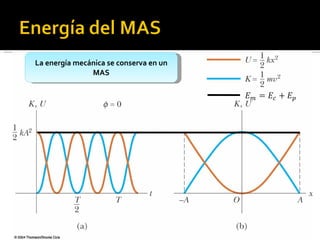
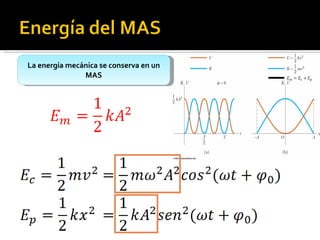
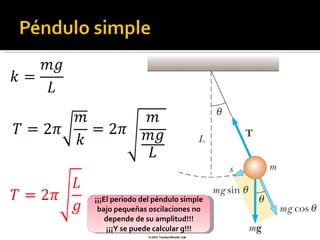
Este documento trata sobre el movimiento armónico simple (MAS), definiéndolo como un movimiento oscilatorio sobre una trayectoria recta sometido a una fuerza proporcional a la distancia al punto de equilibrio. Explica las ecuaciones que rigen el MAS y conceptos clave como periodo, frecuencia y amplitud. También compara el MAS con el movimiento circular uniforme y analiza oscilaciones en péndulos y otros sistemas como lámparas y tocadiscos.

1. Tema 3:

2. Movimiento armónico simple (MAS) Definición Ecuaciones del MAS Comparación con el MCU. Oscilador armónico simple Dinámica Energía Péndulo simple Otras vibraciones Oscilaciones amortiguadas Oscilaciones forzadas Resonancia

3. Vídeo de péndulo Foucault El fenómeno se desarrolla con calma; es inevitable, irresistible ... Viéndolo nacer y crecer, nos damos cuenta de que no está en la mano del observador acelerarlo o frenarlo ... Todo el mundo, en su presencia ... se queda pensativo y callado durante unos instantes y por lo general se va con una sensación más apremiante e intensa de nuestra incesante movilidad en el espacio.

4. Movimiento periódico : Variables cinemáticas se repiten a intervalos regulares ( periodo )

5. Vídeo de péndulo (periódico)

6. Movimiento vibratorio u oscilatorio : desplazamiento periódico sucesivo a uno y otro lado de una posición de equilibrio Vídeo de lámpara oscilando Lámpara de Galileo (Duomo de Pisa)

7. Generalización del concepto oscilación Variación periódica de cualquier magnitud física: campo eléctrico, magnético…

8. Movimiento armónico simple : movimiento oscilatorio sobre trayectoria recta sometido a la acción de una fuerza “tipo Hooke” Vídeo de tocadiscos y lápiz

9. Animación MCU proyectado a MAS

10. Animación de MAS

11. Ley de Hooke Solución armónica

12. Periodo : tiempo que tarda la partícula en realizar una oscilación completa. Amplitud : valor máximo de la elongación. Elongación : distancia que separa al móvil del punto de equilibrio en cada instante. Fase : argumento de la función armónica. Es adimensional, se mide en radianes . Determina la elongación en función de t. Centro de oscilación : punto medio de la distancia que separa las dos posiciones extremas.

13. Unidad SI Hz=s -1 Unidad SI rad/s El seno es una función periódica con periodo Frecuencia: número de oscilaciones por unidad de tiempo. Frecuencia angular o pulsación: número de periodos en unidades de tiempo. ¡¡¡T, f y ω son independientes de A!!!

14. Fase inicial: se mide en radianes, será necesario cuando la posición inicial no coincide con la de equilibrio. Ejemplo:

15. Animación de desfases en MAS

16. La posición máxima se produce cuando el seno se hace 1, es decir que su argumento es π /2 t (s) ω t (rad) sen ω t x(m) 0 0 0 0 T/4 π /2 +1 +A T/2 π 0 0 3T/4 3 π /2 -1 -A T 2 π 0 0

18. La velocidad máxima se produce cuando el coseno se hace 1, es decir que su argumento es nulo t (s) ω t (rad) cos ω t v(m/s) 0 0 +1 +A ω T/4 π /2 0 0 T/2 π -1 -A ω 3T/4 3 π /2 0 0 T 2 π +1 + A ω

19. Vídeo de x, v y a en MAS

20. La aceleración máxima se produce cuando el seno se hace -1, es decir que su argumento es 3 π /2 t (s) ω t (rad) sen ω t a(m/s 2 ) 0 0 0 0 T/4 π /2 +1 -Aω 2 T/2 π 0 0 3T/4 3 π /2 -1 Aω 2 T 2 π 0 0

21. La aceleración es una función oscilante armónica con un desfase de π rad con respecto a la posición.

23. La solución armónica de la ecuación diferencial también podría haber sido un coseno, que está desfasado π /2 con respecto al seno.

24. La fuerza que produce un MAS es central ( dirección ), atractiva ( sentido hacia el punto de equilibrio ) y proporcional a la distancia al punto de equilibrio. Ley de Hooke 2ª Ley de Newton

25. La pulsación, el periodo y la frecuencia de un MAS dependen de la masa y la constante recuperadora del muelle, pero no de la amplitud

26. La energía mecánica se conserva en un MAS

27. La energía mecánica se conserva en un MAS

28. Animación de energías en MAS

29. Animación de péndulo simple

30. Un péndulo simple consiste en un hilo inextensible y de masa despreciable, de longitud L , del que se cuelga una masa puntual m y se le hace oscilar en el vacío. El péndulo se comportará realizará un MAS si se somete a pequeñas oscilaciones ( θ ~ O) .

31. ¡¡¡ El periodo del péndulo simple bajo pequeñas oscilaciones no depende de su amplitud !!! ¡¡¡Y se puede calcular g!!!

32. Vídeos de resonancia, MAS amortiguado y forzado