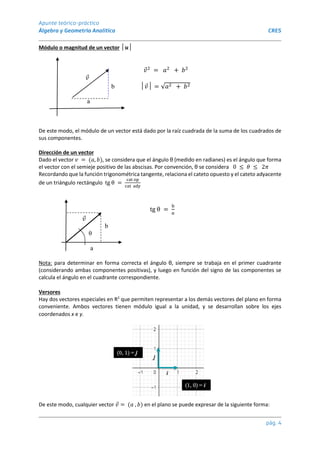
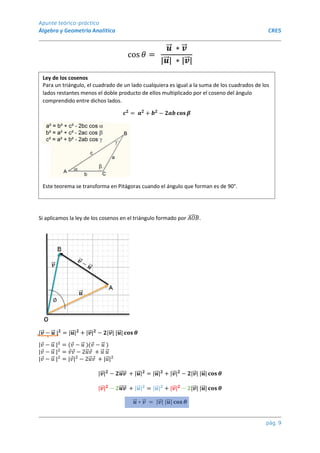
Este documento presenta una introducción al álgebra vectorial. Define vectores como segmentos orientados que tienen magnitud, dirección y sentido. Explica cómo representar vectores en el plano mediante pares ordenados y cómo calcular su magnitud y dirección. También describe operaciones básicas entre vectores como suma, resta, multiplicación por escalares y producto escalar. Finalmente, enumera propiedades clave de estas operaciones algebraicas.










![Apunte teórico-práctico
Álgebra y Geometría Analítica CRES
pág. 13
Dirección de un vector no nulo en R3
Para definir la dirección de un vector en R3, en términos de ciertos ángulos, consideremos el
vector 𝑣 , con origen en O (origen de coordenadas) y extremo en el punto P. 𝑃 = (𝑥0 ,
𝑦0 , 𝑧0 ). De este modo 𝑣 = 𝑂𝑃
⃗⃗⃗⃗⃗
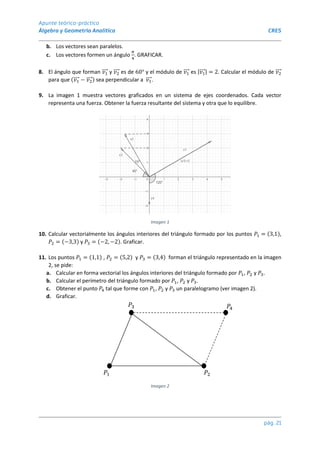
Consideremos además los siguientes ángulos:
α: ángulo entre 𝑣 y el semieje positivo de x (0,0,z0)
β: ángulo entre 𝑣 y el semieje positivo de y
γ: ángulo entre 𝑣 y el semieje positivo de z P = (x0,y0,z0)
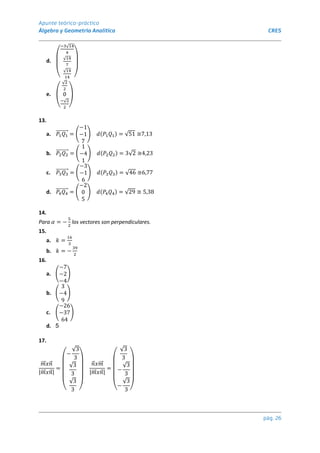
γ β
Estos ángulos se denominan ángulos directores
α (0,y0,0)
(x0,0,0)
Si consideramos que este vector 𝑣 es un vector unitario, es decir │𝑣│ = 1
Entonces:
𝑐𝑜𝑠 𝛼 = 𝑥0 𝑐𝑜𝑠 𝛽 = 𝑦0 𝑐𝑜𝑠 𝛾 = 𝑧0
Por definición, cada uno de estos tres ángulos se encuentra en el intervalo [0, 𝜋]
Los cosenos de estos ángulos reciben el nombre genérico de cosenos directores del vector 𝑣.
Demostraremos que:
cos2
α + cos2
β + cos2
γ = 1
𝑥2
+ 𝑦2
+ 𝑧2
|𝑣|2
=
𝑥2
+ 𝑦2
+ 𝑧2
𝑥2 + 𝑦2 + 𝑧2
= 1
Si 𝛼, 𝛽 𝑦 𝛾 son tres números (cada uno entre 0 y π) tales que satisfacen la condición dada
anteriormente, entonces determinan en forma única el vector unitario
𝒖 = (𝒄𝒐𝒔 𝜶, 𝒄𝒐𝒔 𝜷, 𝒄𝒐𝒔 𝜸 )
Nota: si 𝑣 = (𝑎, 𝑏, 𝑐) 𝑦 |𝑣| = 1 entonces 𝑎, 𝑏 𝑦 𝑐 reciben el nombre de números directores del
vector v](https://image.slidesharecdn.com/4-lgebravectorial-230615184428-7cc47f13/85/4-Algebra-vectorial-pdf-13-320.jpg)