Este documento describe varios métodos iterativos para resolver ecuaciones en una variable. Brevemente describe los métodos de la bisección, regla falsa, punto fijo, Newton-Raphson, secante y Muller, incluyendo sus algoritmos, diagramas de flujo y consideraciones sobre convergencia.

1. ÉTODOS ITERATIVOS
RA LA RESOLUCIÓN
DE ECUACIONES
EN UNA VARIABLE

2. lEstimación inicial
x0 tal que f(x0) ≅ 0
l Proceso iterativo
x1, x2,..., xk, x* :
f(x*)=0
l Criterio de parada
|f(xk)| < tol ó
dk = |xk+1 - xk| <
tol
Tipos de convergencia
l Error del paso k
ek = |xk - x*| |xk -
xk-1|
l Convergencia lineal
ek+1 / ek cte
l Convergencia
cuadrática
ek+1 / ek2 cte

3. METODO DE LA
BISECCIÓN

4. Teorema de Bolzano
Sea f:A continua  
y sean a,b A
con f(a)f(b) < 0.
Entonces, existe
c [a,b] con f(c) = 0.
a
b
f(b
)
f(a
)

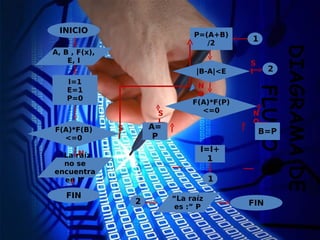
5. Algoritmo de Bisección
c =(a+b)/2;
if f(a)*f(c)<=0 %elige [a,c]
b=c;
end
if f(c)*f(b)<=0 %elige [c,b]
a=c;
endTeorema: El método de la bisección
genera una sucesión {xn} que
converge a una raíz de f con
xn- (b-a)/2n. 

6. DIAGRAMADE
FLUJO
INICIO
A, B , F(x),
E, I
I=1
E=1
P=0
P=(A+B)
/2
F(A)*F(B)
<=0
N
O
S
I
“La raíz
no se
encuentra
en I”
FIN
|B-A|<E
F(A)*F(P)
<=0
S
I
N
O
S
I
N
O
A=
P
B=P
I=I+
1
1
1
2
2 “La raíz
es :” P FIN

7. Método de
Regula-Falsi

8. ¸ Elegir, entre [a,c] y [c,b],
un intervalo en el que la
función cambie de signo.
¹ Repetir los pasos 2 y 3
hasta conseguir la
precisión deseada.
)()( afbf
ab
f(a)ac
−
−
−=
¶ Determinar un intervalo [a,b] tal que
f(a) tiene signo distinto de f(b).
· Hallar el punto c que divide el intervalo
[a,b] en partes proporcionales a f(a) y
f(b). Sea
a
bc

9. Bisección Regula Falsi
K Convergencia lineal
de razón 1/2.
J Cota de la raíz:
(b-a)/2 .
L La aproximación
obtenida puede ser
peor que la del paso
anterior.
J Más rápido al
principio.
K Convergencia lineal.
L Error estimado por:
|xn-xn-1|
L Se aproxima a la
raíz por un lado.
n

10. DIAGRAMADE
FLUJO
INICIO
A, B , F(x),
E, I
I=1
P=A -
F(A)*F(B)
<=0
N
O
SI
“La raíz
no se
encuentra
en I”
FIN
|B-A|<E
F(A)*F(P)
<=0
S
I
N
O
S
I
N
O
A=
P
B=P
I=I+
1
1
2
2 “La raíz
es :” P FIN
F(A)*(B-A)
F(B)-F(A)
T<=I
N
O
S
I
2
1

11. Método del Punto Fijo

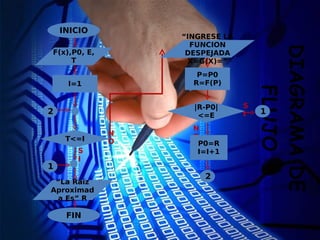
12. ¶ Transformar la ecuación f(x) = 0 en una ecuación
equivalente de punto fijo: x = g(x).
· Tomar una estimación inicial x0 del punto fijo x* de g [x*
punto fijo de g si g(x*) = x*].
¸ Para k=1, 2, 3, … hasta que converja, iterar xn+1 =
g(xn).
Teorema del punto fijo: Sea g:[a,b] [a,b] continua,
entonces:
a) g posee almenos un punto fijo.
b) Si además g’(x) k<1, x [a,b], entonces el punto fijo es  
único y si tomamos x0 [a,b], la sucesión xn+1 = g(xn)

13. Convergencia del Método del
Punto FijoAplicar el método del punto
fijo a:
ò g(x) = cos x, x0
ò g(x) = 2/x2, x0=1
ò g(x) = sqrt(2/x) , x0=1
y analizar los resultados.
Sugerencia: Usar la orden
ITERATES(g(x), x, x0, n)
de DERIVE y comparar los
dos últimos con 2^(1/3).
Tomando x0 cercano al punto
fijo x*
si |g’(x*)| < 1 los iterados
convergen linealmente a x*.
si |g’(x*)| > 1 los iterados no
convergen a x*.
si g’(x*) = 0 los iterados
convergen cuadráticamente a
x*.

14. Algoritmo de Punto Fijo
Datos
Estimación inicial: x0
Precisión deseada: tol
Tope de iteraciones: maxiter
Proceso: mientras no converja repetir
Nueva estimación: x = g(x0)
Incremento: incr = |x - x0|
Actualización: x0 = x
Resultado
Estimación final: x

15. DIAGRAMADE
FLUJO
INICIO
F(x),P0, E,
T
I=1
T<=I
N
O
S
I
“La Raíz
Aproximad
a Es” R
FIN
|R-P0|
<=E
S
I
N
O
1
“INGRESE LA
FUNCION
DESPEJADA
X=G(X)=”
P=P0
R=F(P)
P0=R
I=I+1
2
2
1

16. Método de Newton Rapson

17. l Ecuación de la tangente
l Intersección con OX
l Paso genérico
))((')( 000 xxxfxfy −=−
)x('f)x(fxx 0001 −=
)(')(1 nnnn xfxfxx −=+
(x0, f
(x0))
x1
f(x)

18. Convergencia del método de
Newtonl Newton como iteración de
punto fijo
l Derivada de la función de
iteración
l Convergencia cuadrática
J Ventaja: converge
cuadráticamente si
- la estimación inicial es
buena
- no se anula la derivada
L Inconveniente: usa la
derivada
- coste de la evaluación
- disponibilidad
)x('f)x(fx)xg( −=
2
)('
)(")(
)('g
xf
xfxf
x =
0)('si0)( ≠=
*
xf
*
x'g

19. Algoritmo de Newton
Datos
l Estimación inicial: x
l Precisión deseada: tol
l Tope de iteraciones: maxiter
Proceso: mientras no converja repetir
l Incremento: incr = - f(x)/f’(x)
l Nueva estimación: x = x + incr
Resultado
l Estimación final: x

20. DIAGRAMADE
FLUJO
INICIO
F(x),P0, E,
T
I=1
E=1
T<=I
N
O
S
I
“La Raíz
Aproximad
a Es” P
FIN
|P-P0|
<=E
S
I
N
O
1
P0=P
I=I+1
2
2
P=P0 -
F(P0)
F’(P0)
1

21. METODO DE LA
SECANTE

22. )()( 00 xxmxfy −=−
mxfxx )( 002 −=
01
01
xx
)f(x)f(x
m
−
−
=
l Ecuación de la secante
l Intersección con OX
l Pendiente
x0
x
1
f(x)
x
2
(x1,f(x1)
)
(x0,f(x0
))

23. Algoritmo de la secante
l Datos: x0, x1, y0
l Calcular: y1 = f(x1)
l Calcular: incr = -y1(x1-x0)/(y1-y0)
l Nueva estimación: x2 = x1 + incr
l Actualizar para el paso siguiente:
x0=x1; y0=y1; x1=x2

24. Newton versus Secante
l El método de Newton, cuando converge, lo hace
cuadráticamente, a costa de evaluar la derivada en cada
paso.
l Sin usar la derivada, el método de la secante proporciona
convergencia superlineal.
l Las ecuaciones polinómicas pueden resolverse por el
método de Newton, puesto que la derivada se obtiene
fácilmente.

25. A diferencia del de bisección y regla falsa, casi
nunca falla ya que solo requiere de 2 puntos al
principio, y después el mismo método se va
retroalimentando.
Lo que hace básicamente es ir tirando rectas
secantes a la curva de la ecuación que se tiene
originalmente, y va chequeando la intersección de
esas rectas con el eje de las X para ver si es la raíz
que se busca.

26. DIAGRAMADE
FLUJO
INICIO
F(x),A,B,
E, T
I = 1
E = 1
T<=I
N
O
S
I
“La Raíz
Aproximad
a Es” C
FIN
|A-B|
<=E
S
I
N
O
1
A = B
B = C
I=I+1
2
2
1
C = B -
(B - A) *
F(B)F(B) – F(A)

28. Método de
Steffensen

29. ACELERADOR DE
CONVERGENCIA AITKEN
P=P0
Pn+1=G(P)
Pn+2=G(Pn+1)
Pn = Pn -
(Pn+1-pn)^2
(Pn+2-2Pn+1+P)
El método de Aitken puede ser usado para acelerar
la convergencia de cualquier sucesión que converja
linealmente, independientemente de su origen.

30. AITKEN PUNTO FIJO

33. DIAGRAMADE
FLUJO
INICIO
F(x),P0, E,
T
I = 1
T<=I
N
O
S
I
“La Raíz
Aproximad
a Es” P
FIN
|R-P|
<=E
S
I
N
O
1
“INGRESE LA
FUNCION
DESPEJADA
X=G(X)=”
P=RRR
I=I+1
2
2
1
P=P0
R=G(P)
RR=G(R)
RRR= RR -(RR-R)^2
(RR-R)-(R-P)

34. MÉTODO DE MULLER

35. Consideraciones
Este es un método para encontrar las
raíces de ecuaciones polinomiales de
la forma general:
Donde n es el orden del polinomio y
las son coeficientes constantes.
Continuando con los polinomios, estos
cumplen con las siguientes reglas:
n
nn xaxaxaaxf ++++= .......)( 2
210

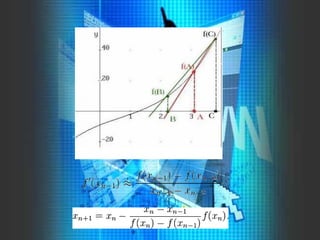
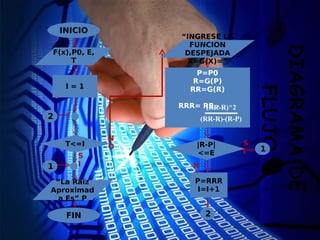
36. El método de Müller, trabaja de manera
similar al método de la secante, pero en lugar
de hacer la proyección de una recta
utilizando dos puntos, requiere de tres puntos
para calcular una parábola.
Para esto necesitaremos de tres puntos [x0,
f(x0)], [x1, f(x1)] y [x2, f(x2)]. La
aproximación la podemos escribir como:
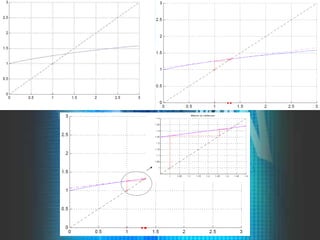
El método consiste en obtener los coeficientes
de los tres puntos, sustituirlos en la fórmula
cuadrática y obtener el punto donde la
parábola intercepta el eje x. La aproximación

37. MÉTODO DE
MULLER
MÉTODO DE LA
SECANTE

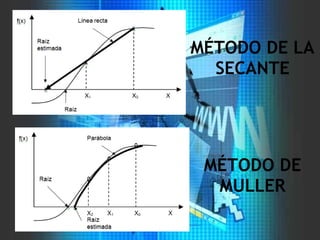
38. se busca esta parábola para intersectar los tres
puntos [x0, f(x0)], [x1, f(x1)] y [x2, f(x2)]. Los
coeficientes de la ecuación anterior se evalúan al
sustituir uno de esos tres puntos para dar:
La última ecuación genera que, , de esta forma, se
puede tener un sistema de dos ecuaciones con dos
incógnitas:
cxxbxxaxf +−+−= )()()( 20
2
200
cxxbxxaxf +−+−= )()()( 21
2
211
cxxbxxaxf +−+−= )()()( 22
2
222
)()()()( 20
2
2020 xxbxxaxfxf −+−=−
)()()()( 21
2
2121 xxbxxaxfxf −+−=−

39. Definiendo de esta forma:
Sustituyendo en el sistema:
Teniendo como resultado los coeficientes:
010 xxh −= 121 xxh −=
01
21
0
)()(
xx
xfxf
−
−
=δ
12
12
1
)()(
xx
xfxf
−
−
=δ
1100
2
1010 )()( δδ hhahhbhh +=+−−
11
2
11 δhahbh =−
01
01
hh
a
+
−
=
δδ
11 δ+= ahb )( 2xfc =

40. Hallando la raíz, se implementar la solución
convencional, pero debido al error de
redondeo potencial, se usará una formulación
alternativa:
La gran ventaja de este método es que se
pueden localizar tanto las raíces reales como
las imaginarias.
Hallando el error este será:
acbb
c
xx
4
2
223
−±
−
+=
%100
3
23
⋅
−
=
x
xx
Ea
23 xxEa −=

41. INICIO
F(X);
XO,X1,X2,ER
ROR
Error<T
OL
HO=X1-X0
H1=X2-X1
S0=(FX2-FX0)/HO
S1=(FX2-FX1)/H1
A=(S1-S0)/(H1-
HO)
B=A*H1+S1
C=F(X2)
RAÍZ=(B^2-
4AC)^0.5
AUS=|B + RAÍZ|
AUS2=|B - RAÍZ|
AUS>AU
S2
SI
X3=X2+((-
2*C)/AUS)
X3=X2+((-
2*C)/AUS2)
ERROR=|X3-X2|
X0=X1
X1=X2
X2=X3
“La Raíz
Aproximada
Es” X3
N
O
1
1
2
2
N
O
SI
3
3
FIN
DIAGRAMADE
FLUJO

42. MÉTODO DE LIN
BAIRSTOW

43. Consideraciones
En análisis numérico, el método de Bairstow
es un algoritmo eficiente de búsqueda de las
raíces de un polinomio real de grado
arbitrario. Es un método iterativo, basado en
el método de Müller y de Newton Raphson.
Dado un polinonio fn(x) se encuentran dos
factores, un polinomio cuadrático:
El procedimiento general para el método de
Bairstow es:

44. Utilizando el método de NR calculamos f2(x) =
x2 – r0x – s0 y fn-2(x), tal que, el residuo de
fn(x)/ f2(x) sea igual a cero.
Se determinan la raíces f2(x), utilizando la
formula general.
Se calcula fn-2(x)= fn(x)/ f2(x).
Hacemos fn(x)= fn-2(x)
Si el grado del polinomio es mayor que tres
regresamos al paso 2
Si no terminamos
La principal diferencia de este método,
respecto a otros, es que permite calcular
todas las raíces de un polinomio (reales e

45. Al dividir entre f2(x) =
x2 – rx – s, tenemos
como resultado el
siguiente polinomio
fn-2(x) = bnxn-2 + bn-
1xn-3 + … + b3x + b2
con un residuo R =

46.
donde los valores de r y s están
dados y calculamos los
incrementos dr y ds que hacen
a b1(r+dr, s+ds) y b0(r+dr,
s+dr) igual a cero. El sistema
de ecuaciones que tenemos

47. donde
Sustituyendo término

48. GRACIAS
UNIVERSIDAD NACIONAL HERMILIO VALDIZAN
FACULTAD DE INGENIERIA CIVIL Y ARQUITECTURA
E. A. P. DE INGENIERIA CIVIL
METODOS NUMERICOS
AUTOR: Est. Ing. Civil
SOTELO DE LA TORRE,Christian Orlando
HUÁNUCO - PERU