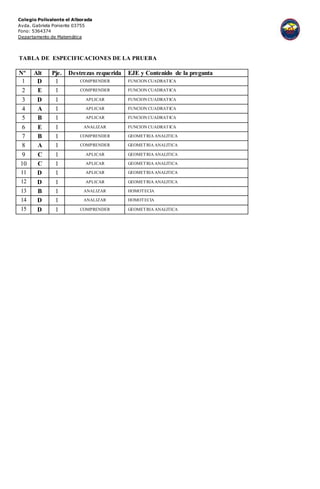
Este documento presenta una prueba de conocimientos previos de matemática para el curso 4° que contiene 15 preguntas. La prueba evalúa objetivos relacionados con ecuaciones cuadráticas, funciones cuadráticas, geometría analítica, puntos medios, distancias entre puntos, homotecias y áreas. El documento también incluye una tabla de especificaciones que relaciona cada pregunta con un objetivo y contenido matemático específico.

1. Colegio Polivalente el Alborada
Avda. Gabriela Poniente 03755
Fono: 5364374
Departamento de Matemática
CONOCIMIENTOS PREVIOS MATEMÁTICA NM4 2018
CONTENIDOS MINIMOS OBLIGATORIOS NM3
Profesora Fresia Cuevas Fuentealba
Nombre
Curso 4° Fecha 2018
Objetivos de aprendizaje:
 Resolver y analizar ejercicios de ecuaciones cuadráticas.
 Aplicar y analizar funciones cuadráticas.
 Calcular distancia entre dos puntos y punto medio de un segmento dado.
 Analizar la razón de homotecia.
 Calcular ecuación de la recta y pendiente.
Instrucciones:
 Esta pruebaconsta de 14 preguntas de selecciónúnica, cada preguntatiene 5opciones,señaladasconlasletras
a, b, c, d y e, una sola de las cuales es la respuesta correcta. (1 punto cada una).
 Las respuestasalas preguntasse marcan enla hoja de respuestas que se le ha entregado. (Complete todos los
datos pedidos, de acuerdo con las instrucciones contenidas en esa hoja. Se le dará tiempo para ello antes de
comenzar la prueba).
 No se permite el uso de calculadora.
I SelecciónMúltiple. Encada uno de lossiguientesejerciciosseleccionelaalternativacorrecta y marque surespuesta en
la cartilla.
1) Los parámetros de lafunción 12)( 2
 xxxf son:
a) a: 1, b:0, c:1
b) a: 2, b:2, c:1
c) a: 2, b:1, c:0
d) a: 1, b:2, c:1
e) No se puede determinar
2) El puntode intersección de la siguiente de lasiguienteparábola 73)( 2
 xxxf conrespectoal eje y,es:
a) Py(0,0)
b) Py(0,2)
c) Py(1,2)
d) Py(1,7)
e) Py(0,7)
3) El puntoo lospuntos,de interseccióncon respectoal eje x, de la siguiente de lasiguienteparábola
12)( 2
 xxxf es o son:
a) Px1(0,1) y Px2(1,0)
b) Px1(-1,1) y Px2(-1,0)
c) Px1(0,-1) = Px2(0,-1)
d) Px1(-1,0) = Px2(-1,0)
e) No se puede determinar.

2. Colegio Polivalente el Alborada
Avda. Gabriela Poniente 03755
Fono: 5364374
Departamento de Matemática
4) El vértice de la siguiente de lasiguienteparábola 12)( 2
 xxxf es;
a) (-1,0)
b) (0,-1)
c) (1,0)
d) (0,1)
e) (0,0)
5) ¿Cuál de lossiguientespuntos Nopertenece a xxxf 2)( 2
 ?
a) (0,0)
b) (-1 ,-3)
c) (2,0)
d) (1,-1)
e) (-2,6)
6) ¿Cuál de lassiguientesfuncionesrepresentalasiguiente grafica?
a) 52)( 2
 xxxf
b) 2
( ) 3 5f x x x  
c)
2
( ) 5 3f x x x   
d) 2
( ) 5 3f x x x  
e) 2
( ) 5 3f x x x  
7) La fórmulaque permite calcularel puntomediode unsegmentodefinidoporlospuntos ),( 11 yxA yel punto
),( 22 yxB es igual a:
a) 






2
;
2
21 yx
PM
b) 




 

2
;
2
2121 yyxx
PM
c) 2
21
2
21 )()( yyxxPM 
d) )()( 2121 yyxxPM 
e) ))(( 2121 yyxxPM 
8) La fórmulaque permite calcularladistanciaentre dospuntos; ),( 11 yxA y ),( 22 yxB esigual a:
a) 2
21
2
21 )()( yyxxd 
b) 






2
;
2
21 yx
d
c) 




 

2
;
2
2121 yyxx
d
d) )()( 2121 yyxxd 
e) ))(( 2121 yyxxd 

3. Colegio Polivalente el Alborada
Avda. Gabriela Poniente 03755
Fono: 5364374
Departamento de Matemática
9) Al determinarel puntomedioentre lospuntos  5;31P y  1;72P resultael punto:
a) (10,6)
b) (4,4)
c) (5,3)
d) (2,2)
e) (-2,-2)
10) Sea 1P (2; 3) y 2P (x;5). ¿Cuántovale x para que tengancomo puntomedioa MP (5; 4)?
a) 2
b) 4
c) 8
d) -4
e) 6
11) ¿Cuál esel área formadapor lospuntos A(0,0),B(12,0) y C(5,4) enun planocartesiano?
a) 64
b) 60
c) 50
d) 24
e) 22
12) ¿Cuál de los siguientespuntospertenece alafunción xxy 32
 ?
a) (-1,-4)
b) (1,4)
c) (0,3)
d) (2,-2)
e) (-2,-10)
13) El triánguloABCde la figuraexperimentaunahomoteciade razón2. Entonces,se producenlossiguientes
efectosenel triánguloresultante:
I: Cambiasu forma
II: Conservasuperímetro
III:Su área se cuadruplica.
a) SoloI
b) SoloIII
c) SoloI y III
d) SoloII y III
e) SoloI y II
B
A C
10 cm
6 cm
8 cm

4. Colegio Polivalente el Alborada
Avda. Gabriela Poniente 03755
Fono: 5364374
Departamento de Matemática
14) Si una figuraexperimentaunahomoteciade razón -0,5.Entonces,se producenlossiguientesefectosen lafigura
resultante:
I: Su área se mantiene constante.
II: Suárea disminuye.
III:Sufre una rotación
a) SoloI
b) SoloII
c) SoloIIII
d) SoloII y III
e) SoloI y II
15) En el gráfico,losejesyel origennose muestran.Si el puntoP tiene coordenadas(5,12) ¿cuálessonlas
coordenadasde Q?
a) (6, 3)
b) (1,10)
c) (8, 15)
d) (8,10)
e) (8,12)

5. Colegio Polivalente el Alborada
Avda. Gabriela Poniente 03755
Fono: 5364374
Departamento de Matemática
TABLA DE ESPECIFICACIONES DE LA PRUEBA
Nº Alt Pje. Destrezas requerida EJE y Contenido de la pregunta
1 D 1 COMPRENDER FUNCION CUADRATICA
2 E 1 COMPRENDER FUNCION CUADRATICA
3 D 1 APLICAR FUNCION CUADRATICA
4 A 1 APLICAR FUNCION CUADRATICA
5 B 1 APLICAR FUNCION CUADRATICA
6 E 1 ANALIZAR FUNCION CUADRATICA
7 B 1 COMPRENDER GEOMETRIA ANALITICA
8 A 1 COMPRENDER GEOMETRIA ANALITICA
9 C 1 APLICAR GEOMETRIA ANALITICA
10 C 1 APLICAR GEOMETRIA ANALITICA
11 D 1 APLICAR GEOMETRIA ANALITICA
12 D 1 APLICAR GEOMETRIA ANALITICA
13 B 1 ANALIZAR HOMOTECIA
14 D 1 ANALIZAR HOMOTECIA
15 D 1 COMPRENDER GEOMETRIA ANALITICA