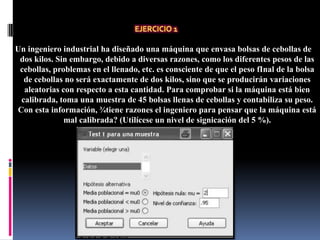
El ingeniero diseñó una máquina para envasar bolsas de cebollas de 2 kg. Tomó una muestra de 45 bolsas y analizó su peso promedio para verificar si la máquina estaba calibrada correctamente. Realizó una prueba t para muestras individuales y encontró que el valor p era mayor al 5%, por lo que no había evidencia suficiente para rechazar la hipótesis nula de que el peso promedio era 2 kg.

1. CONTRASTE DE UNA MEDIA POBLACIONAL

2. Un ingeniero industrial ha diseñado una máquina que envasa bolsas de cebollas de
dos kilos. Sin embargo, debido a diversas razones, como los diferentes pesos de las
cebollas, problemas en el llenado, etc. es consciente de que el peso fInal de la bolsa
de cebollas no será exactamente de dos kilos, sino que se producirán variaciones
aleatorias con respecto a esta cantidad. Para comprobar si la máquina está bien
calibrada, toma una muestra de 45 bolsas llenas de cebollas y contabiliza su peso.
Con esta información, ¾tiene razones el ingeniero para pensar que la máquina está
mal calibrada? (Utilícese un nivel de signicación del 5 %).

3. LA MÁQUINA ESTÁ MAL CALIBRADA
Esta es la afirmación que debemos confirmar
Debemos plasmar la afirmación en la hipótesis alternativa.
tenemos que queremos contrastar
H0 : µ = 2
H1 : µ = 2
Tamaño muestral (45, superior a 30),
RESOLUCIÓN DEL PROBLEMA
MEDIANTE R COMMANDER
Debemos importar los datos desde el chero cebollas.txt para manejar la variable en
cuestión.
A continuación elegimos la opción del menú
ESTADÍSTICOS → MEDIAS → TEST T PARA UNA MUESTRA.

4. Esta opción abrirá la ventana que aparece en la figura
•Nos pide en primer lugar que elijamos una (sólo una) variable, que debe ser
aquella cuya media estemos analizando.
•Nos pide que indiquemos cuál es la hipótesis alternativa. En nuestro caso hemos
elegido la opción de un test bilateral.
•Nos pide que especifiquemos el valor del valor hipotético con el que estamos
comparando la media, en nuestro caso, 2.
•Nos pide, por último, que especifiquemos un nivel de confianza. En realidad este
nivel de confianza no lo es para el contraste, que se resolverá a través del p-valor,
sino para el intervalo de confianza asociado al problema. El enunciado no dice
nada, por lo que ponemos la opción habitual del 95 %.

5. RESULTADO
One Sample t-test
data: Datos$Datos
t = -1.8415, df = 44, p-value = 0.0723
alternative hypothesis: true mean is not equal
to 2
95 percent confidence interval:
1.994974 2.000227
sample estimates:
mean of x
1.9976
.

6. Analisis
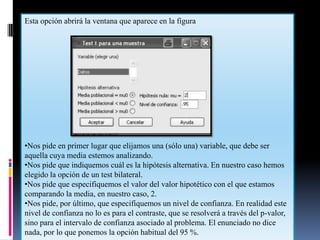
En primer lugar, nos recuerda que estamos analizando la variable Datos$Datos.
A continuación nos informa del valor del estadístico de contraste (t = -1.8415), de
los grados de libertad (df = 44) y del p-valor (p-value = 0.0723). Ya podemos, por
tanto, concluir:
Dado que el p-valor no es inferior al 5 %, no tenemos suficientes evidencias en
los datos para rechazar la hipótesis nula (µ = 2) en favor de la alternativa (µ = 2 6
), es decir, con los datos de la muestra no tenemos suficientes evidencias de que
el peso medio de las bolsas sea distinto de 2.
Nos recuerda cuál era la hipótesis nula que habíamos planteado: alternative
hypothesis: true mean is not equal to 2.
A continuación proporciona un intervalo de confianza unilateral a la derecha, con
un nivel de confianza del 95 %, para la media de la distribución normal que se le
supone a los datos: 95 percent confidence interval: 1.994974 2.000227. Lo que
quiere decir el resultado es que P [µ ∈ (1.994974, 2.000227)] = 0.95.