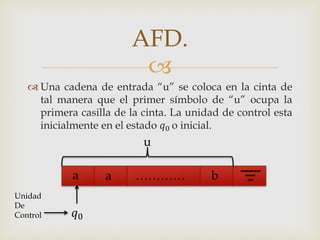
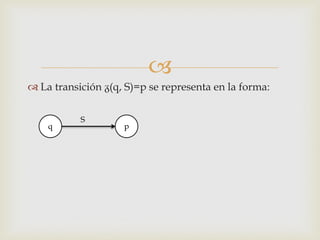
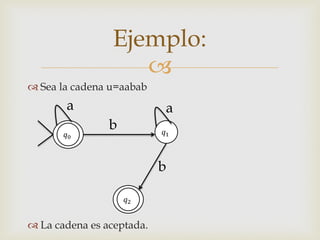
Este documento describe los autómatas finitos deterministas (AFD). Explica que un AFD es una máquina abstracta que procesa cadenas de entrada y las acepta o rechaza dependiendo de si el estado final alcanzado es de aceptación o no. Define los cinco componentes de un AFD y cómo se mueve la unidad de control al leer los símbolos de la cadena de entrada según la función de transición. Finalmente, da un ejemplo para ilustrar el proceso de aceptación de una cadena.

1. Por:
Moisés Morales Guzmán.
Lenguajes y Autómatas.
9no Sem. Ing. Sist. Computacionales.

2. AFD.

Los autómatas finitos son maquinas
abstractas que procesan cadenas de entrada,
las cuales son aceptadas o rechazadas:
Si (u es aceptada).
Cadena de entrada
Autómata M
“u”
No (u no es aceptada).

3. AFD.

 El autómata actúa leyendo los símbolos escritos
sobre una cinta semi-infinita dividida en celdas o
casillas, sobre la cual se escribe una cadena de
entrada u, un símbolo por casilla. El autómata posee
una unidad de control (cabeza lectora o unidad de
memoria) que tiene un numero finito de
configuraciones internas, llamados estados del
autómata.

4. AFD.

 Consideremos el autómata definido por los
siguientes 5 componentes:
 es un conjunto de estados;
 es un alfabeto;
 es el estado inicial;
 es una función de transición;
 es un conjunto de estados finales o de
aceptación.

5. AFD.

 Una cadena de entrada “u” se coloca en la cinta de
tal manera que el primer símbolo de “u” ocupa la
primera casilla de la cinta. La unidad de control esta
inicialmente en el estado ������0 o inicial.
u
a a ………… b
Unidad
De
Control ������0

6. AFD.

La unidad de control de un
autómata siempre se desplaza
hacia la derecha; no puede retornar
ni escribir sobre la cinta.

7. Tablas de transiciones.

 Función de transición S:
ᵹ a B
������0 ������0 ������1
������1 ������1 ������2
������2 ������1 ������1

8. 
ᵹ(������0 ,a)=������0
ᵹ(������1 ,a)=������1
ᵹ(������2 ,a)=������1
ᵹ(������0 ,b)=������1
ᵹ(������1 ,b)=������2
ᵹ(������2 ,b)=������1

9. Ejemplo:

 Sea u=aabab
 ������0 es el estado inicial.
 F = {������0 , ������2 } estados de aceptación.
a a b a b
������0 ������0 ������0 ������1 ������1 ������2
 Como ������2 es un estado de aceptación la cadena es
aceptada.

10. Representación Grafica.

 El estado inicial se representa por:
q
 Los estados finales se representan por:
������0
q
 Los estados se representan por:
q

11. 
 La transición ᵹ(q, S)=p se representa en la forma:
S
q p

12. Ejemplo:

 Sea la cadena u=aabab
a a
b ������1
������0
b
������0
2
 La cadena es aceptada.

13. 