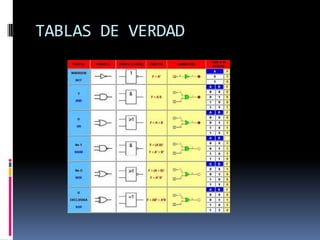
El documento describe la historia y definición del álgebra Booleana. Fue desarrollada por George Boole en el siglo XIX como un sistema matemático centrado en los valores verdadero y falso. Incluye teoremas básicos, operadores lógicos como AND, OR y NOT, y tablas de verdad.

1. ALGEBRA BOOLEANA

2. HISTORIA
 Se denomina así en honor a George Boole ,
matemático inglés autodidacta, que fue el
primero en definirla como parte de un sistema
lógico, inicialmente en un pequeño folleto: The
Mathematical Analysis of Logic, publicado en
1847, en respuesta a una controversia en curso
entre Augustus De Morgan y Sir William
Hamilton. El álgebra de Boole fue un intento de
utilizar las técnicas algebraicas para tratar
expresiones de la lógica proposicional. Más tarde
como un libro más importante: The Laws of
Thought, publicado en 1854.

3. DEFINICION
 Es un sistema matematico centrado en los valores
cero y uno (Falso y verdadero). Son usadas
ampliamente en
el diseño de circuitos de distribución y computadoras
, y sus aplicaciones van en aumento en muchas otras
áreas. En el nivel de lógica digital de
una computadora, lo que comúnmente se
llama hardware, y que está formado por los
componentes electrónicos de la máquina, se trabaja
con diferencias de tensión, las cuales
generan funciones que son calculadas por los
circuitos que forman el nivel. Éstas funciones, en la
etapa de diseña del hardware, son interpretadas
como funciones de boole.

4. TEOREMAS BASICOS
 Ley Distributiva  1A = A
A (B+C) = AB+AC  1+A = 1
 A+A = A  0A = 0
AA = A
 Redundancia
A+AB = A
 A (A+B) = A
 0+A = A

5. OPERADORES BOOLEANOS
 Localizan registros que contienen los
terminos coincidentes en uno de los campos
especificados o en todos los campos
especificados. Utilizar operadores booleanos
para conectar palabras o frases entre mas de
un campo de texto, o utilizar operadores
booleanos para conectar palabras o frases
dentro de un campo de texto.

6. Operador AND (*, .)
 Este operador produce el valor verdadero
sólo si ambos operados son Verdadero. Si
cualquiera de los dos operados es falso,
entonces el resultado es falso.

7. Operador OR (+)
 Este operador realiza una operación o-
inclusivo. El resultado es Verdadero si
cualquiera de los dos operados, o ambos son
Verdadero. En caso contrario es falso.

8. Operador NOT(‘)
 Este operador produce el contrario del
operado. Si el operado es Falso, el resultado
es Verdadero; si el operado es verdadero, el
resultado será falso.
A Y
0 1
1 0

9. TABLAS DE VERDAD

10. POSTULADOS
 Ley conmutativa. Un operador binario (*) para un
conjunto S es conmutativo siempre que: x*y =
y*x para toda x,y pertenecientes a S.
 Ley asociativa. El operador binario (*) es un
conjunto S es asociativo siempre que
x*y*z = x*(y*z) para toda x, y pertenecientes a S.
 Ley distributiva. Si el operador (*) y el operador (.),
son operadores binarios de S, (*) se dice que es
distributivo sobre (.).
 Inversa. El conjunto S tiene un elemento identidad
(e) con respecto al operador (*) siempre que para
cada x perteneciente a S exista un elemento y
perteneciente a S tal que x*y=e.