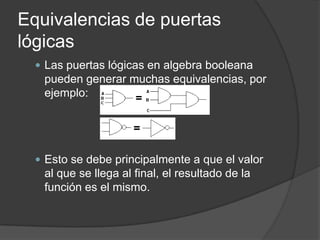
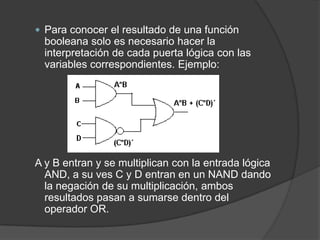
Este documento define el álgebra de Boole y describe sus principios fundamentales. El álgebra de Boole incluye lógica proposicional, álgebra de conjuntos, álgebra de interruptores, tablas de verdad y diagramas de Venn. También describe cómo las operaciones de suma y multiplicación en los circuitos eléctricos corresponden a la unión y el producto en el álgebra de Boole, respectivamente. Además, explica conceptos clave como elementos neutros, conmutatividad, asociatividad y distribución.

1. INSTITUTO TECNOLOGICO DE TIJUANA
Vázquez Torreblanca Rubén
Eric Juárez

2. Definición de Algebra Booleana
 Son un conjunto de reglas matemáticas
que tienen la virtud de que
corresponden a el comportamiento de
circuitos basados en dispositivos de
conmutación tales como interruptores y
transistores.
 El algebra booleana abarca los temas
de lógica proposicional, algebra de
conjuntos y de swiches, tablas de la
verdad y diagrama de Venn.

3. Temas que abarca
 El algebra booleana abarca los temas
de:
 Lógica proposicional
 Algebra de conjuntos
 Algebra de swiches
 Tablas de la verdad
 Diagrama de Venn.

4. Circuitos de conmutación
 Operaciones
 Los valores que pueden tomar los swiches
son solo dos [0,1], estos son los 2 valores
 En circuitos la suma es equivalente a las
conexiones en paralelo.
 En circuitos la multiplicación es equivalente
a las conexiones en serie.

5.  Existencia de neutros:
 Para la suma el elemento neutro es un
circuito abierto [0].
○ Ejemplo: 1+0=1 A+0=A -- El 0 se ignora
 Para el producto (multiplicación) en
elemento neutro es un circuito cerrado [1].
○ Ejemplo: 1*0=0 1*A=A -- El 1 se ignora.
 Conmutatividad:
 El orden en que se coloquen los circuitos,
entradas o espiches no alterara el resultado
final si las conexiones se mantienen.
○ Ejemplo: A+B=B+A

6.  Asociatividad:
 Las conexiones en serie y paralelo son
asociativas ya que no importa cual se
conecte primero. Proviene de la regla de
asociación de A+(B+C)=B+(A+C).
 Distributiva:
 La conexión en serie es distributiva sobre la
conexión en paralelo y viceversa.
 A+(B*C)= (A+B)*(A+C)
 A(B+C)= (A*B)+(A*C)

7. Compuestas Lógicas
 Son la representación de funciones lógicas
mediante símbolos. Se representan con un
conjunto de entradas (variables), la puerta
lógica y la salida. Existen 3 principales:
 And (representa la multiplicación “A*B”)
 Or (representa la suma “A+B”)
 Not (negación lógica B´)
 Adamas de las puertas Nor, Nand, Exor, No-
Exor

8. Equivalencias de puertas
lógicas
 Las puertas lógicas en algebra booleana
pueden generar muchas equivalencias, por
ejemplo:
 Esto se debe principalmente a que el valor
al que se llega al final, el resultado de la
función es el mismo.

9.  Para conocer el resultado de una función
booleana solo es necesario hacer la
interpretación de cada puerta lógica con las
variables correspondientes. Ejemplo:
A y B entran y se multiplican con la entrada lógica
AND, a su ves C y D entran en un NAND dando
la negación de su multiplicación, ambos
resultados pasan a sumarse dentro del
operador OR.