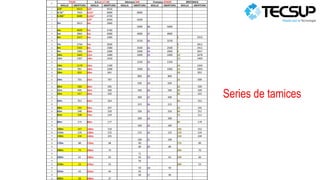
El documento presenta información sobre series de tamices normalizadas y sus características. Explica que las series se estandarizan con una relación de raíz cuadrada de 2 para la serie normal y de 2 para la serie doble. Además, describe las principales normas de tamices de diferentes países e incluye tablas comparativas con las aberturas estandarizadas.

1. ANÁLISIS GRANULOMÉTICO

2. REPRESENTACIÓN GRÁFICA DE
TAMAÑO POR FERET
X
Las series de tamices se encuentran
estandarizadas con una relación:
a) De √2 para la serie normal.
b) De para la serie doble.
2

3. SERIES DE TAMICES
NORMA PAÍS DENOMINACIÓN ESCALA CARACTERÍSTICA
Tyler Malla internacional (**) Relación de tamices dada
en tabla posterior (*)
26,9 mm – 37 µm Razón de raíz cuadrada
de 2.
ASTM U.S.A. Especificación ASTM
(Tabla posterior)
125mm – 38 µm U.S.A. serie de tamices
Standard Canadá 8 –Gp – 1d 125 mm -38 µm Standard tamices
canadienses
AFNOR Francesa AFNOR X -11 - 501 5 mm – 40 µm French Standard
Specifications
BS Gran Bretaña BS 410.62 3.35 mm – 45 µm British Standard
Institution
DIN Alemana DIN 4188 25 mm – 40 µm German Standard
Specifications
UNE 7050 España Relación de tamices 125 mm – 40 µm Legislación española

4. SERIES DE
TAMICES
EE.UU. Gran Bretaña Francia Alemania
ASTM E-11-70 I. B. N. – BS-410 AFNOR X - 11 - 501 DIN 4188
Tamaño o Nº Abertura Nº Abertura Nº Abertura Designación Abertura
mm. mm. mm. µm. mm.
4'' 101,6
3'' 76,1
2 ½'' 64,0
2'' 50,8
1 ¾'' 45,3
1 ½'' 38,1
1 ¼'' 32,0
1'' 25,4 25,0
3/4'' 19,0 20,0
18,0
5/8'' 16,0 16,0
1/2'' 12,7 12,5
3/8'' 9,51 10,0
5/16'' 8,00 8,0
1/4'' Nº 3 6,35 6,3
Nº
4 4,76 38 5,000 5,0
5 4,00 37 4,000 4,0
6 3,36 5 3,353
7 2,83 6 2,812 36 3,150 3,15
8 2,38 7 2,411 35 2,500 2,50
10 2,00 8 2,057 34 2,000 2,00
12 1,68 10 1,676 33 1,600 1,60
14 1,41 12 1,405 32 1,250 1,25
16 1,19 14 1,204
18 1,00 16 1,003 31 1,000 1,00
20 0,841 18 0,853
25 0,707 22 0,699 30 0,800 800 0,800
30 0,595 25 0,599 29 0,630 630 0,630
35 0,500 30 0,500 28 0,500 500 0,500
40 0,420 36 0,422 27 0,400 400 0,400
45 0,354 44 0,353 26 0,315 315 0,315
50 0,297 52 0,295
60 0,250 60 0,251 25 0,250 250 0,250
70 0,210 72 0,211 24 0,200 200 0,200
80 0,177 85 0,780 23 0,160 160 0,160
100 0,149 100 0,152
120 0,125 120 0,124 22 0,125 125 0,125
140 0,105 150 0,104 21 0,100 100 0,100
170 0,088 170 0,089 90 0,090
20 0,080 80 0,080
200 0,074 200 0,076 71 0,071
230 0,063 240 0,066 19 0,063 63 0,630
56 0,056
270 0,053 300 0,053 18 0,050 50 0,050
325 0,044 17 0,040 45 0,045
400 0,037 40 0,040

5. TAMICES DE LA SERIE
TAYLER
Se lee lo resaltado en rojo, 4 hilos horizontales
se cruzan con 4 hilos verticales:

6. TAMICES DE LA SERIE
TAYLER
Las series de tamices se encuentran
estandarizadas con una relación:
Tiene como referencia la malla 200.
La abertura de la malla 200 es de 74
micrómetros (74 µm)
La determinación de la malla es cuantas
aberturas u orificas existen por pulgada línea, a
esto se le conoce como número MESH.

7. TAMICES DE LA SERIE
TAYLER
Las series de tamices se encuentran
estandarizadas con una relación:
Tiene como referencia la malla 200.
La abertura de la malla 200 es de 74
micrómetros (74 µm)
La determinación de la malla es cuantas
aberturas u orificas existen por pulgada línea, a
esto se le conoce como número MESH.

8. SERIE DE TAMICES ASTM
Serie de tamices ASTM
Nótese la diferencia entre las
características de la serie Tyler con
la serie ASTM
Existen ciertas relaciones entre las
aberturas de una malla de la serie
Tyler con respecto de la serie
ASTM.

9. SERIE DE TAMICES ASTM
SERIE ASTM 25.4 1.189207115 1.414213562
SIEVE In mm Serie doble Serie simple
4 0.1870 4.7498 0.1870 0.1870
5 0.1570 3.9878 0.1572
6 0.1320 3.3528 0.1322 0.1322
7 0.1110 2.8194 0.1112
8 0.0937 2.3800 0.0935 0.0935
10 0.0787 1.9990 0.0786
12 0.0661 1.6789 0.0661 0.0661
14 0.0555 1.4097 0.0556
16 0.0469 1.1913 0.0468 0.0468
18 0.0394 1.0008 0.0393
20 0.0331 0.8407 0.0331 0.0331
25 0.0280 0.7112 0.0278
30 0.0232 0.5893 0.0234 0.0234
35 0.0197 0.5004 0.0197
40 0.0165 0.4191 0.0165 0.0165
45 0.0138 0.3505 0.0139
50 0.0117 0.2972 0.0117 0.0117
60 0.0098 0.2489 0.0098
70 0.0083 0.2108 0.0083 0.0083
80 0.0070 0.1778 0.0069
100 0.0059 0.1499 0.0058 0.0058
120 0.0049 0.1245 0.0049
140 0.0041 0.1041 0.0041 0.0041
170 0.0035 0.0889 0.0035
200 0.0029 0.0737 0.0029 0.0029

10. SERIE DE TAMICES

11. TAMICES DE LA SERIE
TAYLER
m = L + d
L
m d
L = “Luz” de la malla
d = Diámetro del alambre de tejido
m = Ancho de la malla
n = Número de malla
n =
𝟏
𝒎
d2 =
𝟏
𝒏𝟐

12. Calcular la caracteristica de un tamiz que tiene una luz de malla de 2.54
y un diametro de alambre de 0.1mm
Ejercicio 1

13. Ejercicio 2
Calcular la luz de malla de un tamiz cuyo número de mallas es de 4 y el
diámetro del alambre de 0.1mm. De acuerdo con el resultado anterior
determinar el número del tamiz.

14. Series de tamices
N°
TYLER U.S.(A.S.T.M) Alemana DIN Francesa AFNOR BRITÁNICA
MALLA ABERTURA MALLA ABERTURA MALLA ABERTURA MALLA ABERTURA MALLA ABERTURA
1 3/8" 9423 3/8" 9510
2 5/16" 7925 5/16" 8000 8000
3 0,265" 6680 0,265" 6730
4 1/4" 6350 6300
5 3m 5613 3m 5660
6 5000 38 5000
7 4m 4699 4m 4760
8 5m 3962 5m 4000 4000 37 4000
9 6m 3327 6m 3360 5 3353
10 3150 36 3150
11 7m 2794 7m 2830 6 2812
12 8m 2355 8m 2380 2500 35 2500 7 2411
13 9m 1981 10m 2000 2000 34 2000 8 2057
14 10m 1665 12m 1680 1600 33 1600 10 1678
15 12m 1397 14m 1410 12 1405
16 1250 32 1250
17 14m 1178 16m 1190 14 1204
18 16m 991 18m 1000 1000 31 1000 16 1003
19 20m 833 20m 841 18 853
20 800 30 800
21 24m 701 25m 707 22 699
22 630 29 630
23 28m 589 30m 595 25 599
24 32m 495 35m 500 500 28 500 30 500
25 35m 417 40m 420 35 422
26 400 27 400
27 42m 351 45m 354 44 353
28 315 26 315
29 48m 295 50m 297 52 295
30 60m 248 60m 250 250 25 250 60 251
31 65m 208 70m 210 72 211
32 200 24 200
33 80m 175 80m 177 85 178
34 160 23 160
35 100m 147 100m 150 100 152
36 115m 124 120m 125 125 22 125 120 124
37 150m 104 140m 105 150 104
38 100 21 100
39 170m 88 170m 98 90 170 89
40 80 20 80
41 200m 74 200m 74 200 70
42 71
43 230m 61 230m 63 63 19 63 240 66
44 56
45 270m 53 270m 53 300 53
46 50 18 50
47 325m 43 325m 44 45
48 40 17 40
49 400m 38 400m 37

15. REPRESENTACIÓN DE DATOS DE UN
ANÁLISIS GRANULOMÉTRICO
MALLA
#
Abertura de malla
(x)
Porcentaje en
masa
f(x)
Porcentaje en
masa acumulado
G(x)
Porcentaje en masa
acumulado pasante
F(x)
x - - 100
x1 f(x1) G(x1) F(x1)
x2 f(x2) G(x2) F(x2)
. . . .
. . . .
xn-1 f(xn-1) G(xn-1) F(xn-1)
xn f(xn) G(xn) F(xn)
SE CUMPLE: G(X) +F(X) = 100

16. FUNCIÓN DISTRIBUCIÓN DE TAMAÑOS
Los resultados de los análisis granulométrico son expresados mediante
funciones que gobierna el tamaño de las partículas en función a la
abertura del tamiz.
Para la determinación de la función distribución se utilizan el porcentaje
en peso f(x) como expresión de frecuencia de un tamaño “x” aparece en
la muestra a la cual se realizo el análisis granulométrico.
De esta manera f(x)dx es el porcentaje en peso de las partículas entre
tamaños “x” y “x”+dx.

17. Función distribución de tamaños
En consecuencia se debe cumplir que la suma de los porcentajes en peso deberá
ser 100% o también
Restringiendo al ecuación anterior a:
Donde F(x) representa el porcentaje en peso de partículas con tamaños
menores a “x”, es decir un porcentaje acumulado pasante
……(1)
……(2)

18. Función distribución de tamaños
La relación entre F(x) y f(x) esta dada por:
La cual se puede deducir derivando la ecuación 2:
G(x) =
Expresa el porcentaje acumulado o porcentaje de partículas de tamaño
mayor a “x”.
……(3)
……(4)

19. Función distribución de tamaños
El tamaño medio de la partícula de una distribución f(x) puede ser calculado como:
Y la varianza queda determinada por:
……(5)
……(6)

20. Función de distribución
Gates - Gaudin – Schuhmann (GGS)
Presenta la siguiente expresión matemática:
Donde:
X0 es el tamaño máximo de la distribución Y.
α es una constante
La forma común de graficar esta función es buscar la ecuación de recta en una
gráfica log –log, en Excel.
La recta se origina tomando logaritmos a ambas partes
……(7)

21. Función de distribución
Gates - Gaudin – Schuhmann (GGS)
Tomando logaritmo a ambas partes:
X Tamaño de partícula
F(x) Porcentaje acumulado pasante
10
100
1000
100
10
Xo
α=tgθ
θ
log=
𝟏𝟎𝟎
𝑿𝒐
α
……(8)

22. Función de distribución
Gates - Gaudin – Schuhmann (GGS)
Derivando: 𝑓 𝑥 = 𝐹´ 𝑥 = 100
𝑋𝑜
α(𝑥)α−1
𝐹(𝑥) = 100( 𝑋
𝑋𝑜
)α
……(9)
Utilizando la ecuación 5 determinamos el tamaño medio de partícula:
µ=
α
α+1
𝑋𝑜 ……(10)
Utilizando la ecuación 6 determinamos la varianza:
σ2 = α𝑋𝑜
α
(α+2)(α+1)2
……(11)

23. APLICACIÓN DE DISTRIBUCIÓN
GATES - GAUDIN – SCHUHMANN (GGS)
La ecuación de G-G-S: 𝐹(𝑥) = 100( 𝑋
𝑋𝑜
)𝛼
La ecuación de la recta queda establecida como:
Transformando a lineal en forma logarítmica según la expresión:
𝐥𝐨𝐠𝑭 𝒙 = 𝜶 𝒍𝒐𝒈 𝒙 + 𝒍𝒐𝒈𝟏𝟎𝟎
𝑿𝒐
𝜶
𝒀 = 𝒃𝑿 + 𝒂
Donde “a” y “b” son:
El coeficiente de correlación esta dado por:
α = b= 𝑁 σ 𝑋𝑌 − σ 𝑋 σ 𝑌
𝑁 σ 𝑋2 − (σ 𝑋)2
r = 𝑁 σ 𝑋𝑌 − σ 𝑋 σ 𝑌
(𝑁 σ 𝑋2 − σ 𝑋 2)(𝑁 σ 𝑌2 − (σ 𝑌)2)
a=
σ 𝑋𝑖
2 σ 𝑌𝑖 − σ 𝑋 σ 𝑋𝑌
𝑁 σ 𝑋2 − (σ 𝑋)2

24. GRACIAS POR SU ATENCIÓN

25. BIBLIOGRAFIA
• Chia Aquije, J. (1985) Operaciones unitarias en procesamiento de minerales. Lima.
• Manzaneda Cabala, José (2000). Procesamiento de mineral chancado, molienda,
flotación, diseño experimental, microscopia. Lima
• Minerals processing comes of age. (May 1, 2009). PACE (Process & Control
Engineering.
• Mular, Andrew L. (2002) Mineral Processing plant design. Vol. 1 New York: American
Institute of Minning.
• Mular, Andrew L. (2002) Mineral Processing plant design. Vol. 2 New York: American
Institute of Minning.
• Rivera Zeballos, Juan H. (2003) Compendio de comunicación. Lima.
• Wills, B.A. (1994). Tecnología de procesamiento de minerales. Tratamiento de minas.
México D.F.: Limusa .
• Lynch A.J. Circuitos de trituración y molienda de minerales.