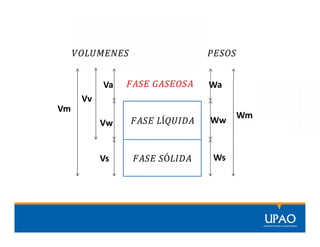
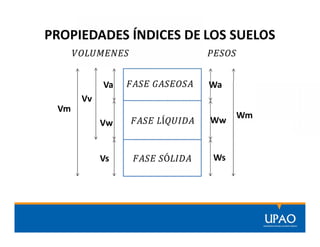
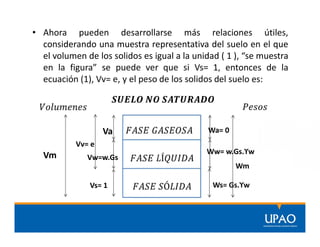
El documento presenta las propiedades, índices y relaciones fundamentales de los suelos, incluyendo volúmenes, pesos, peso específico, porosidad, grado de saturación, humedad, densidad relativa y más. Define cada término y presenta fórmulas para calcular valores como peso específico húmedo, seco y saturado usando datos como peso de la muestra, volumen de sólidos, agua y vacíos. Incluye tres ejercicios de aplicación de las fórmulas.

1. TEMA: INTRODUCCIÓN AL CURSO
Ms. Ing. Alvaro F. Salazar Perales
Trujillo – Perú
CURSO: MECÁNICA DE SUELOS I

2. PROPIEDADES ÍNDICES DE LOS SUELOS
Va
Vw
Vs
Vv
Vm
Wa
Wm
Ww
Ws

3. Donde:
Vm = Volumen total de la muestra del suelo (Volumen de masa).
Vs = Volumen de la fase sólida de la muestra (Volumen de sólidos).
Vv = Volumen de los vacíos de la muestra de suelo (Volumen de
vacíos).
Vw = Volumen de la fase liquida contenida en la muestra (Volumen de
agua).
Va = Volumen de la fase gaseosa de la muestra (Volumen de aire).
Wm = Peso total de la muestra de suelo.
Ws = Peso total de la fase sólida de la muestra de suelo (Peso de
sólidos).
Ww = Peso total de la fase líquida de la muestra (Peso de agua).
Wa = Peso total de la fase gaseosa de la muestra, considerado cero de
Mecánica de Suelos.

4. RELACIONES DE PESOS Y VOLUMENES
ϒ = =
+
Peso Específico de la Masa del suelo (ϒm)
ϒ =
Peso Específico del solido (ϒs)
Peso Específico Relativo de la Masa del suelo
=
ϒ
=
∗ ϒ
=
+
∗ ϒ
…(1)
…(2)
…(3)

5. Peso Específico Relativo de las Partículas
Sólidas ( Gs )
G =
ϒ
=
∗ ϒ
= ϒ ≈ ϒ
NOTA: El valor de ϒ , difiere poco del ϒ y en casos prácticos, ambos
son tomados como iguales .
…(4)
ϒs= Peso Específico de Sólidos
ϒw= Peso especifico del agua.
Nota:ϒw= 1 gr/cm3.
G =

6. RELACIONES FUNDAMENTALES
Relación de Vacíos o Índice de Porosidad (e)
e = En la práctica 0.25 < e < 15
Porosidad (n)
n% = ∗ 100
Grado de Saturación (G).- También se designa con, S (%)
G% = ∗ 100
…(5)
…(6)
…(7)

7. GRADO DE HUMEDAD, W (%)
W% = ∗ (100)
CORRELACIÓN ENTRE LA RELACIÓN DE VACIOS Y LA POROSIDAD
n= e=
CORRELACIÓN ENTRE LA RELACIÓN DE VACIOS Y LA POROSIDAD
ϒ= ∗ ϒ = ∗ ϒ
…(8)
…(9) …(10)
…(11)

8. FÓRMULAS REFERENTES A SUELOS PARCIALMENTE SATURADOS
ϒm= ∗ ϒ =
∗
∗ ϒ G% =
% ∗
PESO ESPECIFICO SECO Y SATURADO
ϒd= ϒsat=
PESO VOLUMÉTRICO DEL SUELO SUMERGIDO ( ϒm)
ϒ´m= ϒ − ϒ
ϒ´m= ∗ ϒ =
∗
∗ ϒ
…(12) …(13)
…(14) …(15)
…(16)
…(17)

9. DENSIDAD RELATIVA DE SUELOS O COMPACIDAD RELATIVA
D % = ∗ (100)
El estado de densidad de los suelos arenosos, puede ser
expresado numéricamente por la fórmula empírica de TERZAGHI,
determinable en laboratorio.
Donde:
emax = Relación de vacíos del suelo en su estado más suelto.
emin. = Relación de vacíos del suelo en el estado más compacto.
e = Relación de vacíos del suelo en el estado natural.
Por otra parte, tenemos según el “Bureau of Reclamation” la fórmula
empírica siguiente:
…(18)

10. D % =
ϒ . (ϒ ϒ . )
ϒ (ϒ . ϒ . )
∗ (100)
Donde:
ϒd.max = Peso Específico seco, en su estado más compacto.
ϒd.min. = Peso Específico seco del suelo en su estado más suelto.
ϒd = Peso Específico seco “in situ”.
…(19)

11. Algunas consideraciones
Cuando una masa de suelo está completamente
saturada (es decir, todo el volumen de vacíos
está lleno de agua), el peso especifico húmedo
de un suelo (ecuación 14) resulta igual al peso
especifico saturado (ϒsat)
• Entonces: ϒ= ϒsat, si Vv= Vw.

12. • Ahora pueden desarrollarse más relaciones útiles,
considerando una muestra representativa del suelo en el que
el volumen de los solidos es igual a la unidad ( 1 ), “se muestra
en la figura” se puede ver que si Vs= 1, entonces de la
ecuación (1), Vv= e, y el peso de los solidos del suelo es:
Va
Vw=w.Gs
Vs= 1
Vv= e
Vm
Wa= 0
Wm
Ww= w.Gs.ϒw
Ws= Gs.ϒw

13. • Gs= Peso especifico relativo de los solidos del suelo o
densidad.
• ϒm= Peso especifico del agua
De la ecuación (…8) el peso del agua Ww= w.Ws. Entonces para
la muestra del suelo bajo consideraciones, Ww=w.Ws= e.Gs.ϒw.
Ahora, para la relación general del peso unitario húmedo dado
en la ecuación (…14), se tiene:
ϒ= = =
.ϒ ( ) …(20)

14. ϒd= = =
.ϒ
Similarmente, el peso especifico seco de la ecuación (…8), se
puede expresar de la siguiente manera:
De la ecuaciones (20) y (21), se obtiene lo siguiente:
…(21)
ϒd=
ϒ
…(22)

15. Vs= 1
Vw=W.Gs= eVv=e
Ww= w.Gs.ϒw= e.ϒw
Ws= Gs.ϒw
También, para este caso:
Vv=
ϒ
=
. .ϒ
ϒ
= . …(23)

16. Entonces, tenemos:
e= . …(24)
El peso especifico saturado del suelo es:
…(25)
ϒsat= =
.ϒ .ϒ

17. Relaciones similares a las ecuaciones (20), (21) y (25) en
términos de la porosidad , también se obtiene considerando una
muestra de suelo respectivamente con volumen unitario. Estas
relaciones son las siguientes:
ϒ= . ϒ (1 − )(1 + ) …(26)
ϒd = . ϒ (1 − ) …(27)
ϒsat= [(1 − )( + )] ∗ ϒ …(28)

18. Ejercicio N° 01
Una muestra de arcilla saturada pesa 1,526gr. y
1,053 gr. después de secada al horno. Calcule su
W (%). Considerando ϒs= 2.70 gr. /cm3. Calcule
también e, n,ϒm.

19. Va
Vw
Vs
Vv
Vm
Wa
Wm
Ww
Ws

20. Ejercicio N° 02
• Una muestra de arena totalmente seca llena
un cilindro metálico de 220 cm3 y pesa 260gr
(Ws), teniendo Gs= 2.6. Calcular e.
Ejercicio N° 03
• El contenido de agua de un suelo saturado es
40%. El Gs de sus partículas es 2.65. Calcular
“e” y ϒm.