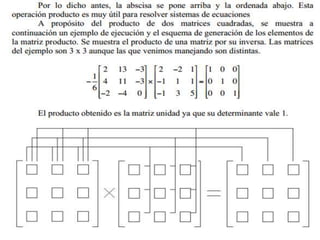
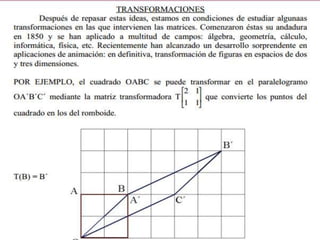
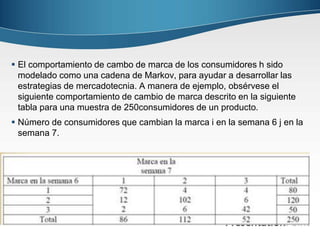
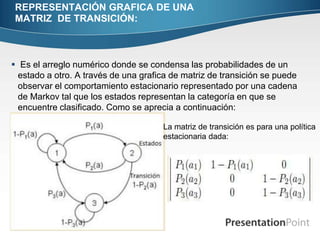
Las matrices se utilizan ampliamente en gráficos 3D, sistemas de ecuaciones y operaciones algebraicas. Las cadenas de Markov y las matrices de transición representan procesos estocásticos y se usan para modelar el comportamiento de los consumidores entre marcas. El wronskiano identifica si funciones son linealmente independientes para ecuaciones diferenciales.