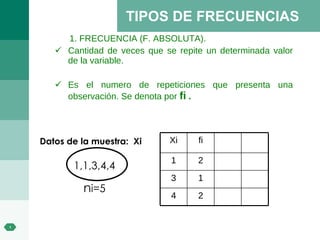
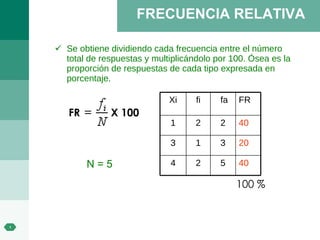
El documento habla sobre la bioestadística y su importancia para la toma de decisiones en el sector de la salud. Explica que la estadística descriptiva se usa para describir y resumir datos, mientras que la estadística inferencial permite hacer estimaciones y predicciones a partir de muestras de datos. También define conceptos clave como población, muestra, variable, frecuencia y medidas de tendencia central y dispersión.

1. “ Bioestadística” M.V.Z. ROLANDO COBOS JUÁREZ

2. “ Uno de los retos que enfrentan los profesionales de la salud es contar con las herramientas analíticas que permitan el uso adecuado de la información disponible para la toma de decisiones en este sector”

3. Hoy día es casi imposible… … que cualquier medio de difusión, periódico, radio, televisión, etc., no nos aborde diariamente con cualquier tipo de información estadística sobre: accidentes de tráfico, índices de crecimiento de población, turismo, tendencias políticas, etc.

4. Los métodos estadísticos Tienen especial aplicación en el campo de las ciencias biológicas y sociales utilizadas por la medicina. En el estudio de fenómenos que tienen gran variabilidad y que están determinados por factores múltiples.

5. El término estadística tiene su raíz en la palabra Estado. Surge cuando se hace necesario para sus intereses cuantificar conceptos. En la mayoría de los casos esta cuantificación se hará en función de unos fines económicos o militares. El estado quiere conocer censo de personas, de infraestructura, de recursos en general, para poder obtener conclusiones de esta información. Definición de estadística.

6. Actualmente la estadística es una ciencia. No es ya una cuestión reservada al estado. Podríamos decir que se encuentra en la totalidad del resto de ciencias. La razón es clara: por una parte la estadística proporciona técnicas precisas para obtener información, (recogida y descripción de datos) y por otra parte proporciona métodos para el análisis de esta información .

7. De ahí el nombre de ESTADÍSTICA DESCRIPTIVA , ya que el objetivo será, a partir de una muestra de datos (recogida según una técnica concreta), la descripción de las características más importantes, entendiendo como características, aquellas cantidades que nos proporcionen información sobre el tema de interés del cual hacemos el estudio.

8. La estadística . Se ocupa de los métodos y procedimientos para recoger, clasificar, resumir, y analizar los datos, así como de realizar inferencias a partir de ellos, con la finalidad de ayudar a la toma de decisiones y en su caso formular predicciones. Bioestadística. Aplicación de la estadística a los procesos biológicos, incluyendo los de salud.

9. Clasificación Describir, resumir y presentar datos. Muestreo de datos para sacar conclusiones sobre poblaciones más grandes. E. Descriptiva E. Inferencial

10. Estadística descriptiva: Describe, analiza y representa un grupo de datos utilizando métodos numéricos y gráficos que resumen y presentan la información contenida en ellos. Puede ser: Aritmética Tabular Gráfica

11. Estadística inferencial Apoyándose en el cálculo de probabilidades y a partir de datos muestrales, efectúa estimaciones, decisiones, predicciones u otras generalizaciones sobre un conjunto mayor de datos.

12. Población Es el conjunto de elementos, individuos o entes sujetos a estudio y de los cuales queremos obtener un resultado. Las poblaciones pueden ser: finitas infinitas

13. Muestra Una muestra . Conjunto de elementos que forman parte de población. La muestra representa a esta población. Tamaño muestral: Es le número de elementos u observaciones que tomamos. Se denota por n ó N.

14. VARIABLE: Es la característica que estamos midiendo. Existen dos categorías o tipo de variables: Variable cualitativa: Es aquella que expresa un atributo o característica, ejemplo: Rubio, moreno, etc. Variable cuantitativa: Es aquella que podemos expresar numéricamente: edad, peso, no. de hijos, etc. Esta a su vez la podemos subdividir en:

15. Variable discreta , aquella que entre dos valores próximos puede tomar a lo sumo un número finito de valores. Ejemplos: el número de hijos de una familia, el de obreros de una fabrica, el de alumnos de la universidad, etc. Variable continua la que puede tomar los infinitos valores de un intervalo. En muchas ocasiones la diferencia es más teórica que práctica, ya que los aparatos de medida dificultan que puedan existir todos los valores del intervalo. Ejemplos, peso, estatura, distancias, etc.

16. La variable se denota por las mayúsculas de letras finales del alfabeto castellano. A su vez cada una de estas variables puede tomar distintos valores , colocando un subíndice, que indica orden. Dato: Cada uno de los individuos, cosas, entes abstractos que integran una población o universo determinado. Dicho de otra forma, cada valor observado de la variable

17. TIPOS DE FRECUENCIAS 1. FRECUENCIA (F. ABSOLUTA). Cantidad de veces que se repite un determinada valor de la variable. Es el numero de repeticiones que presenta una observación. Se denota por fi . 1,1,3,4,4 Datos de la muestra: Xi n i=5 1 3 2 1 2 4 fi Xi

18. Fr ecuencia acumulada. Es la suma de los distintos valores de la frecuencia absoluta tomando como referencia un individuo dado. La última frecuencia absoluta acumulada es igual al nº de casos. Es el conteo del número de veces que ocurre cada respuesta en el conjunto de datos. Es el número de veces que se repite cada dato. (ni,fa) 3 1 3 2 2 1 5 2 4 fa fi Xi

19. FRECUENCIA RELATIVA Se obtiene dividiendo cada frecuencia entre el número total de respuestas y multiplicándolo por 100. Ósea es la proporción de respuestas de cada tipo expresada en porcentaje. FR X 100 N = 5 100 % 20 3 1 3 40 2 2 1 40 5 2 4 FR fa fi Xi

20. Medidas de tendencia central Mediana Moda Media Las medidas de tendencia central corresponden a valores que generalmente se ubican en la parte central de un conjunto de datos. (Ellas permiten analizar los datos en torno a un valor central).

21. Media (media aritmética) Si x 1 , x 2 ,.., x n representan una muestra de tamaño n de la población, la media aritmética se calcula: Sumando todas las observaciones y dividiendo entre el número de observaciones X i = valor de cada observación n = número de observaciones

22. Propiedades La media aritmética es la medida tendencia central que posee menor varianza. Engloba en ella toda la información de la muestra; esto, con ser una ventaja, supone una cierta desventaja pues los valores muy extremos, en muestras pequeñas la afectan.

23. La Mediana Es un medida de posición Es el valor que es mayor o igual que el 50% de las observaciones de la muestra y menor o igual que el otro 50%. Para calcularla se ordenan las observaciones de menor a mayor. Si n es impar , la mediana es la observación central.

24. Si n es par La mediana se define como la media de las dos observaciones centrales.

25. Propiedades: Es única. Es más fácil de calcular que la media aritmética y apenas se afecta por observaciones extremas. Sin embargo tiene mayor varianza que la media y sólo toma en cuenta la información de los valores centrales de la muestra.

26. La moda Es el valor más frecuente . Su cálculo es el más simple de los tres correspondientes a estadísticos de centralidad Es el estadístico de mayor varianza

27. Medidas representativas de un conjunto de datos estadísticos

28. Las medidas de variabilidad tienen por objeto medir la magnitud de los desvíos de los valores de la variable con respecto al valor central de la distribución. Rango Varianza Desviación estándar Coeficiente de variación Medidas de variabilidad o dispersión

29. El Rango Diferencia entre el valor de las observaciones mayor y el menor R = X L - X S

30. La Varianza Mide el grado de dispersión de los datos con referencia a la media aritmética. Es el promedio (media) de los cuadrados de los desvíos de cada observación respecto de la media aritmética:

31. La desviación estándar Es la Raíz Cuadrada de la Varianza:

32. Coeficiente de variación Comparar la variabilidad entre dos grupos de datos referidos a distintos sistemas de unidades de medida. Por ejemplo, kilogramos y centímetros. Comparar la variabilidad entre dos grupos de datos obtenidos por dos o más personas distintas.

33. Coeficiente de Variación Comparar dos grupos de datos que tienen distinta media. Determinar si cierta media es consistente con cierta varianza.

34. GRACIAS POR SU ATENCIÓN